Mouvement brownien
 Mouvement brownien d'une particule.
Mouvement brownien d'une particule.
 Simulation de mouvement brownien pour cinq particules (jaunes) qui entrent en collision avec un lot de 800 particules. Les cinq chemins bleus représentent leur trajet aléatoire dans le fluide.
Simulation de mouvement brownien pour cinq particules (jaunes) qui entrent en collision avec un lot de 800 particules. Les cinq chemins bleus représentent leur trajet aléatoire dans le fluide.
Le mouvement brownien, ou processus de Wiener, est une description mathématique du mouvement aléatoire d'une « grosse » particule immergée dans un liquide et qui n'est soumise à aucune autre interaction que des chocs avec les « petites » molécules du fluide environnant. Il en résulte un mouvement très irrégulier de la grosse particule, qui a été décrit pour la première fois en 1827 par le botaniste Robert Brown en observant les mouvements spontanés de grains de pollen de Clarkia pulchella en suspension, puis de diverses autres plantes.
La description physique la plus élémentaire du phénomène est la suivante :
- entre deux chocs, la grosse particule se déplace en ligne droite avec une vitesse constante ;
- la grosse particule est accélérée lorsqu'elle rencontre une molécule de fluide ou une paroi.
Ce mouvement permet de décrire avec succès le comportement thermodynamique des gaz (théorie cinétique des gaz), ainsi que le phénomène de diffusion. Il est aussi très utilisé dans des modèles de mathématiques financières.
Aspects historiques
Le philosophe et poète latin Lucrèce (60 av. J.-C.) donne une remarquable description du mouvement des particules selon les principes d'Épicure dans son œuvre De la nature des choses :
« Si tu penses que les atomes, principes des choses, peuvent trouver le repos et dans ce repos engendrer toujours de nouveaux mouvements, tu te trompes et t'égares loin de la vérité. Puisqu'ils errent dans le vide, il faut qu'ils soient tous emportés, soit par leur pesanteur propre, soit par le choc d'un autre corps. Car s'il leur arrive dans leur agitation de se rencontrer avec choc, aussitôt ils rebondissent en sens opposés : ce qui n'a rien d'étonnant puisqu'ils sont des corps très durs, pesants, denses, et que rien derrière eux ne les arrête. Et pour mieux comprendre comment s'agitent sans fin tous les éléments de la matière, souviens-toi qu'il n'y a dans l'univers entier aucun fond ni aucun lieu où puissent s'arrêter les atomes, puisque l'espace sans limite ni mesure est infini en tous sens, ainsi que je l'ai montré abondamment avec la plus sûre doctrine. Puisqu'il en est ainsi, il ne peut y avoir aucun repos pour les atomes à travers le vide immense ; au contraire agités d'un mouvement continuel et divers, ils se heurtent, puis rebondissent, les uns à de grandes distances, les autres faiblement, et s'éloignent peu. »
 Mouvement de sphères (20 nm de diamètre) de latex fluorescentes dans de l'eau.
Mouvement de sphères (20 nm de diamètre) de latex fluorescentes dans de l'eau.
À l'été 1827, le naturaliste écossais Robert Brown aperçut dans le fluide situé à l’intérieur des grains de pollen de la Clarkia pulchella, de très petites particules agitées de mouvements apparemment chaotiques et non pas les grains de pollen eux-mêmes comme souvent mentionné. Brown n'est pas exactement le premier à avoir fait cette observation. Il signale lui-même que plusieurs auteurs avaient suggéré l’existence d’un tel mouvement (en lien avec les théories vitalistes de l'époque). Parmi ceux-ci, certains l’avaient effectivement décrit. On peut mentionner en particulier l’abbé John Turberville Needham (1713-1781), célèbre à son époque pour sa grande maîtrise du microscope, qui attribua ce mouvement à une activité vitale.
La réalité des observations de Brown a été discutée tout au long du XXe siècle. Compte tenu de la médiocre qualité de l'optique dont il disposait, certains ont contesté qu'il ait pu voir véritablement le mouvement brownien, qui intéresse des particules de quelques micromètres au plus. Les expériences ont été refaites par l’Anglais Brian Ford au début des années 1990, avec le matériel employé par Brown et dans les conditions les plus semblables possibles. Le mouvement a bien été observé dans ces conditions, ce qui valide les observations de Brown (et justifie le nom de Mouvement Brownien).
En 1901, Louis Bachelier propose un premier modèle mathématique du mouvement brownien et l'applique à la finance.
 Reproduction d'un dessin de Perrin dans Mouvement brownien et réalité moléculaire. Sont représentées ici trois trajectoires de particules de mastic d'environ 1 µm de diamètre. Les positions successives des particules, pointées toutes les 30 secondes, sont reliées par des segments.
Reproduction d'un dessin de Perrin dans Mouvement brownien et réalité moléculaire. Sont représentées ici trois trajectoires de particules de mastic d'environ 1 µm de diamètre. Les positions successives des particules, pointées toutes les 30 secondes, sont reliées par des segments.
En 1905, Albert Einstein donne une description quantitative du mouvement brownien et indique notamment que des mesures faites sur le mouvement permettent d'en déduire leur dimension moléculaire. Jean Perrin réalise ce programme et publie en 1909 une valeur du nombre d'Avogadro, ce qui lui vaut un prix Nobel en 1926. Il décrit également l'extrême irrégularité des trajectoires qui n'ont de tangente en aucun point. On peut trouver un célèbre dessin de Perrin d'observations de particules.
« C’est un cas où il est vraiment naturel de penser à ces fonctions continues sans dérivées que les mathématiciens ont imaginées, et que l’on regardait à tort comme de simples curiosités mathématiques, puisque l’expérience peut les suggérer. »
— Jean Perrin
Dans cette même période, le physicien français Paul Langevin développe une théorie du mouvement brownien suivant sa propre approche (1908).
Norbert Wiener donne une définition mathématique en 1923 en construisant une mesure de probabilité sur l'espace des fonctions continues réelles. Il étudie, de manière mathématique, la continuité et non-dérivabilité des trajectoires du mouvement brownien. Il définit également l'intégrale de Wiener (l'intégrale par rapport au mouvement brownien).
En 1933, Paul Lévy démontre que le mouvement brownien est un cas particulier de martingale continue, notion inventée par Jean Ville en 1933, celui où le carré de ce mouvement soustrait de sa valeur temps reste une martingale. Il démontre également que ce cas particulier est le seul parmi les martingales à avoir ces deux propriétés. Ce faisant, il donne la définition du mouvement brownien, c'est-à-dire ses conditions nécessaires et suffisantes. En 1948, il publie le premier grand ouvrage sur le mouvement brownien Processus stochastiques et mouvement brownien. Il apporte alors de nombreux résultats.
Depuis, des études fines sur le mouvement brownien ont été réalisées par de nombreux auteurs. Citons Volker Strassen ainsi que Kiyoshi Itō, lequel développe un calcul différentiel spécifique au mouvement brownien : le calcul stochastique.
Plus récemment, David Baker et Marc Yor ont démontré, à partir du processus Carr-Ewald-Xiao décrit en 2008, que les descriptions de processus aléatoires temporels et continus, en particulier les flux financiers, par le mouvement brownien procédaient bien souvent d'une naïveté basée sur une définition empirique du mouvement brownien, les aléas ne pouvant pas toujours être définis de manières indépendantes c'est-à-dire que le drap brownien à n dimensions utilisé l'est abusivement dans un phénomène qui ne possède pas ces n dimensions.
Approche mathématique
La difficulté de modélisation du mouvement brownien réside dans le fait que ce mouvement est aléatoire et que statistiquement, le déplacement est nul : il n'y a pas de mouvement d'ensemble, contrairement à un vent ou un courant. Plus précisément :
- à un instant donné, la somme vectorielle des vitesses de toutes les particules s'annule (il n'y a pas de mouvement d'ensemble) ;
- si l'on suit une particule donnée au cours du temps, le barycentre de sa trajectoire est son point de départ, elle « virevolte » autour du même point.
Il est difficile dans ces conditions de caractériser le mouvement. La solution fut trouvée par Louis Bachelier, et présentée dans sa thèse soutenue le 29 mars 1900. Il démontra que ce qui caractérise le mouvement, ce n'est pas la moyenne arithmétique des positions <X> mais la moyenne quadratique ⟨ X 2 ⟩ {\displaystyle {\sqrt {\langle \,X^{2}\,\rangle \ }}} : si x(t) est la distance de la particule à sa position de départ à l'instant t, alors :
⟨ X 2 ( t ) ⟩ = 1 t ∫ 0 t x 2 ( τ ) d τ {\displaystyle \langle \,X^{2}(t)\ \rangle \ =\ {\frac {1}{t}}\int _{0}^{t}x^{2}(\tau )\ d\tau }
On démontre que le déplacement quadratique moyen est proportionnel au temps :
| ⟨ X 2 ( t ) ⟩ = 2 d D t {\displaystyle \langle \,X^{2}(t)\ \rangle \ =\ 2\,d\,D\,t} |
où d est la dimension du mouvement (linéaire, plan, spatial), D le coefficient de diffusion, et t le temps écoulé.
Définition
Un mouvement brownien est une martingale telle que
- cette martingale est continue dans le temps
- son carré soustrait de son temps est une martingale
( M t ) {\displaystyle (M_{t})} est un mouvement brownien si et seulement si ( M t ) {\displaystyle (M_{t})} est une martingale continue telle que ( M t 2 − t ) {\displaystyle (M_{t}^{2}-t)} est une martingale.
Descriptions dimensionnelles
 Approximation d'un mouvement brownien bidimensionnel par une marche aléatoire de 3 000 pas dont chaque pas est gaussien en abscisse et en ordonnée.
Approximation d'un mouvement brownien tridimensionnel par une marche aléatoire de 1 000 pas dont chaque pas est gaussien en abscisse, en ordonnée et en cote.
Approximation d'un mouvement brownien bidimensionnel par une marche aléatoire de 3 000 pas dont chaque pas est gaussien en abscisse et en ordonnée.
Approximation d'un mouvement brownien tridimensionnel par une marche aléatoire de 1 000 pas dont chaque pas est gaussien en abscisse, en ordonnée et en cote.
Définition uni-dimensionnelle
Le mouvement brownien unidimensionnel ( B t ) t ≥ 0 {\displaystyle (B_{t})_{t\geq 0}} est un processus stochastique dépendant du temps t et vérifiant :
- (accroissements indépendants) Quels que soient les temps t et s tels que t > s, l'accroissement B t − B s {\displaystyle B_{t}-B_{s}} est indépendant du processus ( B u ) 0 ≤ u ≤ s {\displaystyle (B_{u})_{0\leq u\leq s}} avant le temps s.
- (accroissements stationnaires et gaussiens) Quels que soient les temps t et s tels que t > s, l'accroissement B t − B s {\displaystyle B_{t}-B_{s}} est une variable aléatoire normale de moyenne nulle et de variance t−s.
- ( B t ) t ≥ 0 {\displaystyle (B_{t})_{t\geq 0}} est presque sûrement continu, c'est-à-dire pour presque toute réalisation, la fonction t ↦ B t ( ω ) {\displaystyle t\mapsto B_{t}(\omega )} est continue.
- Il est souvent supposé que B 0 = 0 {\displaystyle B_{0}=0} . On dit alors que le mouvement brownien est standard.
Définition équivalente
Le mouvement brownien unidimensionnel ( B t ) t ≥ 0 {\displaystyle (B_{t})_{t\geq 0}} est un processus stochastique dépendant du temps t et vérifiant :
- Le processus ( B t ) t ≥ 0 {\displaystyle (B_{t})_{t\geq 0}} est un processus gaussien, c'est-à-dire pour tous temps t 1 ≤ t 2 ≤ . . . ≤ t n {\displaystyle t_{1}\leq t_{2}\leq ...\leq t_{n}} , le vecteur ( B t 1 , B t 2 , . . . , B t n ) {\displaystyle (B_{t_{1}},B_{t_{2}},...,B_{t_{n}})} est un vecteur gaussien.
- ( B t ) t ≥ 0 {\displaystyle (B_{t})_{t\geq 0}} est presque sûrement continu. C'est-à-dire pour toute réalisation, la fonction t ↦ B t ( ω ) {\displaystyle t\mapsto B_{t}(\omega )} est continue.
- pour tous s et t, la moyenne est E = 0 {\displaystyle \mathbb {E} =0} et la covariance est E = min ( s , t ) {\displaystyle \mathbb {E} =\min(s,t)} .
Définition multi-dimensionnelle
Le mouvement brownien d-dimensionnel est un processus ( B t ) t ≥ 0 := ( B t 1 , B t 2 , . . . , B t d ) t ≥ 0 {\displaystyle (B_{t})_{t\geq 0}:=\left(B_{t}^{1},B_{t}^{2},...,B_{t}^{d}\right)_{t\geq 0}} où les processus B 1 , B 2 , . . . , B d {\displaystyle B^{1},B^{2},...,B^{d}} sont des mouvements browniens indépendants.
Autrement dit le mouvement brownien d-dimensionnel est à valeurs dans R d {\displaystyle \mathbb {R} ^{d}} et ses projections sur les espaces R , R 2 , . . . , R d − 1 {\displaystyle \mathbb {R} ,\mathbb {R} ^{2},...,\mathbb {R} ^{d-1}} sont respectivement des mouvements browniens uni-, bi-, ..., d-1-dimensionnels.
Définition de la mesure de Wiener
Considérons C ( R + , R ) {\displaystyle {\mathcal {C}}(\mathbb {R} ^{+},\mathbb {R} )} l'espace des fonctions continues de R + {\displaystyle \mathbb {R} ^{+}} dans R {\displaystyle \mathbb {R} } et ( Ω , T , P ) {\displaystyle (\Omega ,{\mathcal {T}},\mathbb {P} )} un espace probabilisé. Le mouvement brownien est l'application
B : Ω ⟶ C ( R + , R ) ω ↦ ( t ↦ B t ( ω ) ) {\displaystyle {\begin{array}{lccl}B:&\Omega &\longrightarrow &C(\mathbb {R} ^{+},\mathbb {R} )\\&\omega &\mapsto &\left(t\mapsto B_{t}(\omega )\right)\end{array}}} .La mesure de Wiener (ou loi du mouvement brownien), souvent notée W ( d ω ) {\displaystyle W(\mathrm {d} \omega )} , est la mesure-image de P ( d ω ) {\displaystyle \mathbb {P} (\mathrm {d} \omega )} par cette application B.
Autrement dit, c'est la mesure de probabilité W sur C ( R + , R ) {\displaystyle {\mathcal {C}}(\mathbb {R} ^{+},\mathbb {R} )} telle que pour tout A ⊂ C ( R + , R ) {\displaystyle A\subset {\mathcal {C}}(\mathbb {R} ^{+},\mathbb {R} )} ,
W ( A ) = P ( ( B t ) t ≥ 0 ∈ A ) {\displaystyle W(A)=\mathbb {P} ((B_{t})_{t\geq 0}\in A)} .Remarques
- Le mouvement brownien est un processus de Lévy à accroissements gaussiens.
- Cette définition permet de démontrer des propriétés du mouvement brownien, par exemple sa continuité (presque sûre), le fait que presque sûrement, la trajectoire n'est différentiable nulle part, et de nombreuses autres propriétés.
- On pourrait également définir le mouvement brownien par rapport à sa variation quadratique moyenne. Cette définition, classiquement appelée théorème de Lévy, donne la caractérisation suivante: un processus stochastique à trajectoires continues dont la variation quadratique est t est un mouvement brownien. Ceci se traduit mathématiquement par le fait que pour une filtration donnée, ( B t ) t ≥ 0 {\displaystyle (B_{t})_{t\geq 0}} et ( B t 2 − t ) t ≥ 0 {\displaystyle (B_{t}^{2}-t)_{t\geq 0}} sont des martingales.
Propriétés
- Les trajectoires du mouvement brownien sont presque sûrement nulle part dérivables, c'est-à-dire que pour presque tout ω ∈ Ω {\displaystyle \omega \in \Omega } , la fonction t ↦ B t ( ω ) {\displaystyle t\mapsto B_{t}(\omega )} est une fonction continue nulle part dérivable.
- La covariance est donnée par E = min ( s , t ) {\displaystyle \mathbb {E} =\min(s,t)} pour tous réels s et t.
- Le mouvement brownien a la propriété de Markov forte : pour tout temps d'arrêt T, conditionnellement à {\displaystyle } , le processus ( B t T ) t ≥ 0 := ( B T + t − B T ) t ≥ 0 {\displaystyle (B_{t}^{T})_{t\geq 0}:=(B_{T+t}-B_{T})_{t\geq 0}} est un mouvement brownien indépendant du processus ( B s ) 0 ≤ s < T {\displaystyle (B_{s})_{0\leq s<T}} .
- Sa transformée de Fourier ou fonction caractéristique est donnée par E = e − t u 2 2 {\displaystyle \mathbb {E} \left=e^{-{\frac {tu^{2}}{2}}}} . On retrouve le fait que le mouvement brownien soit un processus de Lévy sans drift (« dérive »), sans sauts et de coefficient quadratique 1/2.
- Le mouvement brownien est homogène en temps : pour tout s > 0, ( B t + s − B s ) t ≥ 0 {\displaystyle (B_{t+s}-B_{s})_{t\geq 0}} est un mouvement brownien indépendant de ( B u ) 0 ≤ u ≤ s {\displaystyle (B_{u})_{0\leq u\leq s}} .
- Le processus -B est un mouvement brownien.
- Propriété de stabilité - Pour tout c > 0, le processus ( c B t c 2 ) t ≥ 0 {\displaystyle \left(cB_{\frac {t}{c^{2}}}\right)_{t\geq 0}} est un mouvement brownien. On dit que le mouvement brownien est stable d'indice 2.
- Inversion du temps - Le processus ( t B 1 t ) t > 0 {\displaystyle \left(tB_{\frac {1}{t}}\right)_{t>0}} qui s'annule en t=0 est un mouvement brownien.
- Récurrence Le mouvement brownien d-dimensionnel est récurrent si et seulement si d=1 ou d=2. C'est-à-dire
- Principe de réflexion
Construction mathématique
Donnons d'autres manières de construire le mouvement brownien.
Au moyen du théorème de consistance de KolmogorovSoit ( f t ) t ∈ R + {\displaystyle (f_{t})_{t\in \mathbb {R} _{+}}} une famille de fonctions à valeurs réelles appartenant à L 2 ( R + ) {\displaystyle L^{2}(\mathbb {R} _{+})} . Posons alors :
∀ ( u , v ) ∈ R + 2 , s ( u , v ) = ⟨ f u , f v ⟩ L 2 ( R + ) = ∫ R + f u ( x ) f v ( x ) d x {\displaystyle \forall (u,v)\in \mathbb {R} _{+}^{2}{\text{, }}s(u,v)={\langle f_{u},f_{v}\rangle }_{L^{2}(\mathbb {R} _{+})}=\int _{\mathbb {R} _{+}}f_{u}(x)f_{v}(x)\mathrm {d} x}Alors, la fonction satisfait la propriété suivante :
∀ k ∈ N ∗ {\displaystyle \forall k\in \mathbb {N} ^{*}} et tous t 1 , . . . , t k ∈ R + {\displaystyle t_{1},...,t_{k}\in \mathbb {R} _{+}} , la matrice ( s ( t i , t j ) ) 1 ≤ i , j ≤ k {\displaystyle \left(s(t_{i},t_{j})\right)_{1\leq i,j\leq k}} est symétrique et semi-définie positive.
Au moyen du théorème de consistance de Kolmogorov, on peut construire un processus gaussien { Y t } t ∈ R + {\displaystyle \{Y_{t}\}_{t\in \mathbb {R} _{+}}} dont la fonction moyenne m est arbitraire et dont la fonction de covariance est s définie au-dessus.
Lorsque ( f t ) t ∈ R + = ( c 1 1 ) t ∈ R + {\displaystyle (f_{t})_{t\in {\mathbb {R} _{+}}}=\left({\sqrt {c}}\,1\!\!1_{}\right)_{t\in \mathbb {R} _{+}}} où c > 0 {\displaystyle c>0} est une constante ne dépendant pas de t, et où 1 1 {\displaystyle 1\!\!1_{}} est la fonction indicatrice sur , il résulte de l'expression de s que pour tout ( u , v ) ∈ R + 2 {\displaystyle (u,v)\in {\mathbb {R} _{+}^{2}}} :
s ( u , v ) = c ∫ R 1 1 ( s ) 1 1 ( s ) d s = c min ( u , v ) {\displaystyle s(u,v)=c\int \limits _{\mathbb {R} }1\!\!1_{}(s)1\!\!1_{}(s)\mathrm {d} s=c\,\min(u,v)}Dans ce cas-là, la matrice ( s ( t i , t j ) ) 1 ≤ i , j ≤ k {\displaystyle \left(s(t_{i},t_{j})\right)_{1\leq i,j\leq k}} est symétrique et définie positive pour tout k ∈ N ∗ {\displaystyle k\in \mathbb {N} ^{*}} et t 1 , . . . , t k {\displaystyle t_{1},...,t_{k}} 2 à 2 distincts.
On dit qu'un processus gaussien à valeurs réelles indexé par R + {\displaystyle \mathbb {R} _{+}} est un mouvement brownien lorsque le processus est centré (i.e. l'application t ↦ E X t {\displaystyle t\mapsto \mathbb {E} X_{t}} est identiquement nulle) et que sa fonction de covariance s est donnée ci-dessus. D'habitude, un mouvement brownien est noté par { B t } t ∈ R + {\displaystyle \{B_{t}\}_{t\in \mathbb {R} _{+}}} . Signalons que c = Var ( B 1 ) {\displaystyle c=\operatorname {Var} (B_{1})} . Lorsque c = 1, le mouvement brownien est dit standard.
Au moyen d'une marche aléatoireLe théorème de Donsker (1951) montre qu'une marche aléatoire convenablement renormalisée converge en loi vers le mouvement brownien.
( 1 σ n ( ∑ k = 1 U k + ( n t − ) U + 1 ) ) 0 ≤ t ≤ 1 ⟶ n → ∞ ( B t ) 0 ≤ t ≤ 1 {\displaystyle \left({\frac {1}{\sigma {\sqrt {n}}}}\left(\sum _{k=1}^{}U_{k}+(nt-)U_{+1}\right)\right)_{0\leq t\leq 1}{\underset {n\rightarrow \infty }{\longrightarrow }}(B_{t})_{0\leq t\leq 1}}où est la partie entière et les variables aléatoires (Un, n ≥ 1) sont iid, centrées, de carré intégrable et de variance σ {\displaystyle \sigma } 2. La convergence ⟶ n → ∞ {\displaystyle {\underset {n\rightarrow \infty }{\longrightarrow }}} est la convergence en loi dans l'espace C() des fonctions continues sur muni de sa tribu borélienne.
Cette convergence donne une définition du mouvement brownien comme l'unique limite (en loi) de marches aléatoires renormalisées.
Au moyen d'une série de FourierDonnons une construction du mouvement brownien fondée sur les séries de Fourier.
Soient deux suites indépendantes ( N k , k ∈ N ) {\displaystyle (N_{k},k\in \mathbb {N} )} et ( N k ′ , k ∈ N ) {\displaystyle (N'_{k},k\in \mathbb {N} )} de variables aléatoires indépendantes de loi normale N ( 0 , 1 ) {\displaystyle {\mathcal {N}}(0,1)} . Le processus ( B t ) t ≥ 0 {\displaystyle (B_{t})_{t\geq 0}} défini par la série
B t := t N 0 + ∑ k = 1 + ∞ 2 2 π k ( N k ( cos ( 2 π k t ) − 1 ) + N k ′ sin ( 2 π k t ) ) {\displaystyle B_{t}:=tN_{0}+\sum _{k=1}^{+\infty }{\frac {\sqrt {2}}{2\pi k}}\left(N_{k}(\cos(2\pi kt)-1)+N_{k}'\sin(2\pi kt)\right)}est un mouvement brownien.
Excursion brownienne Article principal : Excursion brownienne. en haut : simulation d'un pont brownien standard.
en haut : simulation d'un pont brownien standard. en bas : simulation d'une excursion brownienne normalisée.
Considérons B := { t ≥ 0 , B t = 0 } {\displaystyle {\mathcal {B}}:=\{t\geq 0,B_{t}=0\}} l'ensemble des zéros du mouvement brownien unidimensionnel (ensemble des temps où le mouvement brownien s'annule). Le complémentaire de B {\displaystyle {\mathcal {B}}} est une suite d'intervalles ouverts que l'on note ⋃ n ≥ 1 B n {\displaystyle \bigcup _{n\geq 1}{\mathcal {B}}_{n}} . Chaque intervalle a une longueur notée | B n | {\displaystyle |{\mathcal {B}}_{n}|} .
Pour chaque n ≥ 1, on définit les processus e n := ( e n ( t ) , 0 ≤ t ≤ | B n | ) {\displaystyle e_{n}:=(e_{n}(t),0\leq t\leq |{\mathcal {B}}_{n}|)} et e n n o r m := ( e n n o r m ( t ) , 0 ≤ t ≤ 1 ) {\displaystyle e_{n}^{norm}:=(e_{n}^{norm}(t),0\leq t\leq 1)} par
e n ( t ) := B t + inf B n {\displaystyle e_{n}(t):=B_{t+\inf {\mathcal {B}}_{n}}} pour tout 0 ≤ t ≤ | B n | {\displaystyle 0\leq t\leq |{\mathcal {B}}_{n}|} , e n n o r m ( t ) := B t | B n | + inf B n | B n | {\displaystyle e_{n}^{norm}(t):={\frac {B_{t|{\mathcal {B}}_{n}|+\inf {\mathcal {B}}_{n}}}{\sqrt {|{\mathcal {B}}_{n}|}}}} pour tout 0 ≤ t ≤ 1 {\displaystyle 0\leq t\leq 1} .e n {\displaystyle e_{n}} est appelée l'excursion brownienne, e n n o r m {\displaystyle e_{n}^{norm}} est l'excursion brownienne normalisée (voir le livre de Itô et McKean).
Les excursions sont soit "au-dessus" de 0 (s'il existe un t tel que e n ( t ) > 0 {\displaystyle e_{n}(t)>0} ) soit "au-dessous" de 0 (s'il existe un t tel que e n ( t ) < 0 {\displaystyle e_{n}(t)<0} ).
Propriétés
- Les excursions ( e n , n ≥ 1 ) {\displaystyle (e_{n},n\geq 1)} sont indépendantes et de même loi. De même pour ( e n n o r m , n ≥ 1 ) {\displaystyle (e_{n}^{norm},n\geq 1)} . e 1 n o r m {\displaystyle e_{1}^{norm}} est markovien avec :
- Les signes des excursions sont indépendantes et de loi P = P = 1 2 {\displaystyle \mathbb {P} =\mathbb {P} ={\frac {1}{2}}} .
- Il existe des liens entre l'excursion brownienne et le pont brownien.
Estimation du nombre d'Avogadro
La formule suivante permet de calculer le coefficient de diffusion d'un couple particule-fluide par la loi de Stokes-Einstein :
D = k B T 6 π η r {\displaystyle D={\frac {k_{B}T}{6\pi \eta r}}}où T est la température, η la viscosité dynamique du fluide, r le rayon de la particule, kB la constante de Boltzmann.
Considérations énergétiques
La quantité d'énergie mise en œuvre par le mouvement brownien est négligeable à l'échelle macroscopique. On ne peut pas en tirer de l'énergie pour réaliser un mouvement perpétuel de seconde espèce, et violer ainsi le deuxième principe de la thermodynamique.
Toutefois, il a été démontré que certains processus biologiques à l'échelle cellulaire peuvent orienter le mouvement brownien afin d'en soutirer de l'énergie. Cette transformation ne contrevient pas au deuxième principe de la thermodynamique tant et aussi longtemps qu'un échange de rayonnement peut maintenir la température du milieu (système dissipatif) donc la vitesse moyenne des particules. Il faut aussi considérer que la dissipation de ce mouvement brownien sous forme d'énergie utilisable engendre une croissance de l'entropie globale du système (ou de l'univers).
Généralisations
- Une généralisation naturelle est la feuille brownienne.
- Une généralisation est le processus de Lévy.
Quelques modélisations dans un espace euclidien
Équation de Langevin (1908)
Article détaillé : Équation de Langevin.Dans l'approche de Langevin, la grosse particule brownienne de masse m animée à l'instant t d'une vitesse v ( t ) {\displaystyle v(t)} est soumise à deux forces :
- une force de frottement fluide du type f = − k v {\displaystyle f\,=\,-\,k\,v} , où k est une constante positive ;
- un bruit blanc gaussien η ( t ) {\displaystyle \eta (t)}
Bruit blanc gaussien :
Un bruit blanc gaussien η ( t ) {\displaystyle \eta (t)} est un processus stochastique de moyenne nulle :⟨ η ( t ) ⟩ = 0 {\displaystyle \langle \,\eta (t)\,\rangle \ =\ 0}
et totalement décorrélé dans le temps ; sa fonction de corrélation à deux points vaut en effet :
⟨ η ( t 1 ) η ( t 2 ) ⟩ = Γ δ ( t 1 − t 2 ) {\displaystyle \langle \,\eta (t_{1})\ \eta (t_{2})\,\rangle \ =\ \Gamma \ \delta (t_{1}-t_{2})}
Dans cette formule, Γ {\displaystyle \Gamma } est une constante positive, et δ ( t ) {\displaystyle \delta (t)} est la distribution de Dirac.
Dans ces deux formules, la moyenne est prise sur toutes les réalisations possibles du bruit blanc gaussien. On peut formaliser ceci en introduisant une intégrale fonctionnelle, encore appelée intégrale de chemin d'après Feynman, définie pour la mesure gaussienne dite « mesure de Wiener ». Ainsi, on écrit :
⟨ η ( t 1 ) η ( t 2 ) ⟩ = ∫ η ( t 1 ) η ( t 2 ) e − 1 2 Γ ∫ t 1 t 2 η ˙ 2 ( τ ) d τ {\displaystyle \langle \,\eta (t_{1})\ \eta (t_{2})\,\rangle \ =\ \int \left\ \eta (t_{1})\ \eta (t_{2})\ {\textrm {e}}^{-{\frac {1}{2\Gamma }}\int _{t_{1}}^{t_{2}}{\dot {\eta }}^{2}(\tau )d\tau }}
où η ˙ {\displaystyle {\dot {\eta }}} est la dérivée de η {\displaystyle \eta } par rapport au temps t.Le principe fondamental de la dynamique de Newton conduit à l'équation stochastique de Langevin :
| m d v ( t ) d t = − k v ( t ) + η ( t ) {\displaystyle m\,{\frac {dv(t)}{dt}}\ =\ -\,k\,v(t)\ +\ \eta (t)} |
Processus d’Ornstein-Uhlenbeck
Article détaillé : Processus d'Ornstein-Uhlenbeck.Le processus d'Ornstein-Uhlenbeck est un processus stochastique décrivant (entre autres) la vitesse d'une particule dans un fluide, en dimension 1.
On le définit comme étant la solution X t {\displaystyle X_{t}} de l'équation différentielle stochastique suivante : d X t = 2 d B t − X t d t {\displaystyle dX_{t}={\sqrt {2}}dB_{t}-X_{t}dt} , où B t {\displaystyle B_{t}} est un mouvement brownien standard, et avec X 0 {\displaystyle X_{0}} une variable aléatoire donnée. Le terme d B t {\displaystyle dB_{t}} traduit les nombreux chocs aléatoires subis par la particule, alors que le terme − X t d t {\displaystyle -{X_{t}}dt} représente la force de frottement subie par la particule.
La formule d'Itô appliquée au processus e t X t {\displaystyle {e^{t}}X_{t}} nous donne : d ( e t X t ) = e t X t d t + e t ( 2 d B t − X t d t ) = e t 2 d B t {\displaystyle d({e^{t}}X_{t})={e^{t}}{X_{t}}dt+{e^{t}}({\sqrt {2}}{dB_{t}}-{X_{t}}dt)={e^{t}}{\sqrt {2}}{dB_{t}}} , soit, sous forme intégrale : X t = X 0 e − t + 2 e − t ∫ 0 t e s d B s {\displaystyle X_{t}={X_{0}}e^{-t}+{\sqrt {2}}e^{-t}\int _{0}^{t}{e^{s}}dB_{s}}
Par exemple, si X 0 {\displaystyle X_{0}} vaut presque sûrement x {\displaystyle x} , la loi de X t {\displaystyle X_{t}} est une loi gaussienne de moyenne x e − t {\displaystyle xe^{-t}} et de variance 1 − e − 2 t {\displaystyle 1-e^{-2t}} , ce qui converge en loi quand t {\displaystyle t} tend vers l'infini vers la loi gaussienne centrée réduite.
Marches aléatoires
Article détaillé : Marche aléatoire.On peut aussi utiliser un modèle de marche aléatoire (ou au hasard), où le mouvement se fait par sauts discrets entre positions définies (on a alors des mouvements en ligne droite entre deux positions), par exemple dans le cas de la diffusion dans les solides. Si les xi sont les positions successives d'une particule, alors on a après n sauts :
| ⟨ X n 2 ⟩ = 1 n ∑ i = 1 n x i 2 {\displaystyle \langle \,X_{n}^{2}\ \rangle \ =\ {\frac {1}{n}}\ \sum _{i=1}^{n}\ x_{i}^{2}} |
Marche aléatoire à une dimension d'espace (Exemple)
Considérons la marche aléatoire d'une particule sur l'axe Ox. On suppose que cette particule effectue des sauts de longueur a entre deux positions contigües situées sur le réseau : { n a , n ∈ Z } {\displaystyle \{\,n\,a\ ,n\in \mathbb {Z} \,\}} de maille a sur l'axe, chaque saut ayant une durée τ {\displaystyle \tau } .
Il faut encore se donner un nombre p tel que : 0 < p < 1. L'interprétation physique de ce paramètre est la suivante :
- p représente la probabilité que la particule fasse un saut vers la droite à chaque instant ;
- q = 1 - p représente la probabilité que la particule fasse un saut vers la gauche à chaque instant.
Le cas du mouvement brownien correspond à faire l'hypothèse d'isotropie spatiale. Toutes les directions de l'espace physique étant a priori équivalentes, on pose l'équiprobabilité :
| p = q = 1 2 {\displaystyle p\ =\ q\ =\ {\frac {1}{2}}} |
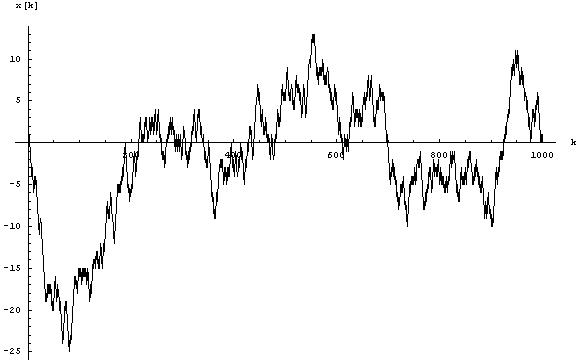
La figure ci-dessous montre un exemple typique de résultat : on trace les positions successives x(k) de la particule aux instants k, partant de la condition initiale x(0)=0.
Probabilités de transition conditionnelleOn définit la probabilité de transition conditionnelle :
| P ( n | m , s ) = P ( n a | m a , s τ ) {\displaystyle P(n|m,s)\ =\ P(na|ma,s\tau )} |
comme étant la probabilité de trouver la particule au site ma à l'instant s τ {\displaystyle s\tau } sachant qu'elle était au site na à l'instant initial 0.
L'hypothèse d'isotropie conduit à écrire la loi d'évolution de cette probabilité de transition conditionnelle :
| P ( n | m , s + 1 ) = 1 2 {\displaystyle P(n|m,s+1)\ =\ {\frac {1}{2}}\ \left} |
On en déduit la relation suivante :
| P ( n | m , s + 1 ) − P ( n | m , s ) = 1 2 {\displaystyle P(n|m,s+1)\,-\,P(n|m,s)\ =\ {\frac {1}{2}}\ \left} |
Prenons la limite continue de l'équation précédente lorsque les paramètres :
- τ → 0 {\displaystyle \tau \ \to \ 0}
- a → 0 {\displaystyle a\ \to \ 0}
On verra à la fin du calcul que la combinaison a 2 / 2 τ {\displaystyle a^{2}/2\tau } doit en fait rester constante dans cette limite continue.
Il vient, en réintroduisant le paramètre adéquat pour faire un développement limité :
| P ( n | m , ( s + 1 ) τ ) − P ( n | m , s τ ) = τ ∂ P ( n | m , s τ ) ∂ t + O ( τ 2 ) {\displaystyle P(n|m,(s+1)\tau )\ -\ P(n|m,s\tau )\ =\ \tau \ {\frac {\partial P(n|m,s\tau )}{\partial t}}\ +\ O(\tau ^{2})} |
D'autre part, on peut écrire :
| P ( n | ( m ± 1 ) a , s ) = P ( n | m a , s ) ± a ∂ P ( n | m a , s ) ∂ x + a 2 2 ∂ 2 P ( n | m a , s ) ∂ x 2 + O ( a 3 ) {\displaystyle P(n|(m\pm 1)a,s)\ =\ P(n|ma,s)\,\pm \,a\ {\frac {\partial P(n|ma,s)}{\partial x}}\,+\,{\frac {a^{2}}{2}}\ {\frac {\partial ^{2}P(n|ma,s)}{\partial x^{2}}}\,+\,O(a^{3})} |
de telle sorte que le crochet se réduise à :
| P ( n | m + 1 , s ) + P ( n | m − 1 , s ) − 2 P ( n | m , s ) = a 2 ∂ 2 P ( n | m a , s ) ∂ x 2 + O ( a 3 ) {\displaystyle P(n|m+1,s)\,+\,P(n|m-1,s)\,-\,2\ P(n|m,s)\ =\ a^{2}\ {\frac {\partial ^{2}P(n|ma,s)}{\partial x^{2}}}\,+\,O(a^{3})} |
On en déduit l'équation de Fokker-Planck :
| τ ∂ P ( x 0 | x , t ) ∂ t = a 2 2 ∂ 2 P ( x 0 | x , t ) ∂ x 2 {\displaystyle \tau \ {\frac {\partial P(x_{0}|x,t)}{\partial t}}\ =\ {\frac {a^{2}}{2}}\ {\frac {\partial ^{2}P(x_{0}|x,t)}{\partial x^{2}}}} |
qu'on peut réécrire :
| ∂ P ( x 0 | x , t ) ∂ t = D ∂ 2 P ( x 0 | x , t ) ∂ x 2 {\displaystyle {\frac {\partial P(x_{0}|x,t)}{\partial t}}\ =\ D\ {\frac {\partial ^{2}P(x_{0}|x,t)}{\partial x^{2}}}} |
en introduisant le coefficient de diffusion :
| D = a 2 2 τ {\displaystyle D\ =\ {\frac {a^{2}}{2\tau }}} |
En plus de l'équation de Fokker-Planck, la densité de probabilité de transition conditionnelle P ( x 0 | x , t ) {\displaystyle P(x_{0}|x,t)} doit vérifier les deux conditions supplémentaires suivantes :
- la normalisation des probabilités totales :
| ∀ t > 0 , ∫ − ∞ + ∞ d x P ( x 0 | x , t ) = 1 {\displaystyle \forall \ t\ >\ 0\ ,\quad \int _{-\infty }^{+\infty }dx\ P(x_{0}|x,t)\ =\ 1} |
- la condition initiale :
| lim t → 0 P ( x 0 | x , t ) = δ ( x − x 0 ) {\displaystyle \lim _{t\to 0}P(x_{0}|x,t)\ =\ \delta (x-x_{0})} |
où δ ( x ) {\displaystyle \delta (x)} est la distribution de Dirac.
La densité de probabilité de transition conditionnelle P ( x 0 | x , t ) {\displaystyle P(x_{0}|x,t)} est donc essentiellement une fonction de Green de l'équation de Fokker-Planck. On peut démontrer qu'elle s'écrit explicitement :
| P ( x 0 | x , t ) = 1 4 π D t exp {\displaystyle P(x_{0}|x,t)\ =\ {\frac {1}{\sqrt {4\pi Dt}}}\ \exp \,\left} |
Moments de la distribution :
Posons x 0 = 0 {\displaystyle x_{0}=0} pour simplifier. La densité de probabilité de transition conditionnelle P 0 ( x , t ) = P ( 0 | x , t ) {\displaystyle P_{0}(x,t)=P(0|x,t)} permet le calcul des divers moments :⟨ x n ( t ) ⟩ = ∫ − ∞ + ∞ d x x n P 0 ( x , t ) {\displaystyle \langle \,x^{n}(t)\ \rangle \ =\ \int _{-\infty }^{+\infty }dx\ x^{n}\ P_{0}(x,t)}
La fonction P 0 {\displaystyle P_{0}} étant paire, tous les moments d'ordre impair sont nuls. On peut facilement calculer tous les moments d'ordre pair en posant :
α = 1 4 D t {\displaystyle \alpha \ =\ {\frac {1}{4Dt}}}
et en écrivant que :
⟨ x 2 n ( t ) ⟩ = α π ∫ − ∞ + ∞ d x x 2 n e − α x 2 = ( − 1 ) n α π d n d α n {\displaystyle \langle \,x^{2n}(t)\ \rangle \ =\ {\sqrt {\frac {\alpha }{\pi }}}\ \int _{-\infty }^{+\infty }dx\ x^{2n}\ \mathrm {e} ^{-\alpha x^{2}}\ =\ (-1)^{n}\ {\sqrt {\frac {\alpha }{\pi }}}\ {\frac {d^{n}~}{d\alpha ^{n}}}\ \left}
On obtient explicitement :
⟨ x 2 n ( t ) ⟩ = ( − 1 ) n α π d n d α n = ( − 1 ) n α d n d α n {\displaystyle \langle \,x^{2n}(t)\ \rangle \ =\ (-1)^{n}\ {\sqrt {\frac {\alpha }{\pi }}}\ {\frac {d^{n}~}{d\alpha ^{n}}}\ \left\ =\ (-1)^{n}\ {\sqrt {\alpha }}\ {\frac {d^{n}~}{d\alpha ^{n}}}\ \left}
On retrouve notamment pour le moment d'ordre deux :
⟨ x 2 ( t ) ⟩ = − α d d α = ( − α ) × ( − 1 2 α 3 / 2 ) = 1 2 α = 2 D t {\displaystyle \langle \,x^{2}(t)\ \rangle \ =\ -\,{\sqrt {\alpha }}\,{\frac {d~}{d\alpha }}\,\left\ =\ (-\,{\sqrt {\alpha }})\,\times \,\left(-\,{\frac {1}{2\alpha ^{3/2}}}\right)\ =\ {\frac {1}{2\alpha }}\ =\ 2Dt}
Mouvement brownien sur une variété riemannienne
On appelle mouvement brownien sur une variété riemannienne V le processus stochastique continu markovien dont le semigroupe de transition à un paramètre est engendré par 1 / 2 Δ V {\displaystyle 1/2\,\Delta _{V}} , où Δ V {\displaystyle \Delta _{V}} est l'opérateur de Laplace-Beltrami sur la variété V .
Notes et références
- Robert Brown ; A brief account of microscopical observations made in the months of June, July and August, 1827, on the particles contained in the pollen of plants; and on the general existence of active molecules in organic and inorganic bodies., Philosophical Magazine 4 (1828), 161-173. Fac-similé disponible au format pdf.
- Brian J. Ford ; Brownian movement in Clarkia pollen: a reprise of the first observations, The Microscope, 40 (4): 235-241, 1992 Reproduction en ligne de l'article.
- F. Hirsch & al., Peacocks ans associated martingales with explicit constructions, Bocconi & Springer, 2011.
- Pour un mouvement rectiligne régulier, c'est le déplacement x(t) qui serait proportionnel au temps.
- (en) K. ITO et H.P. McKean, Diffusion Processes and their sample paths : Reprint of the 1974 Edition, Berlin, Springer Verlag - Classics in Mathematics, 1974, 2e éd., 323 p., poche (ISBN 978-3-540-60629-1, LCCN 95049024, lire en ligne).
- (PESKIN C. S. (1); ODELL G. M.;OSTER G. F.;Biophysical journal (Biophys. j.), CODEN BIOJAU; 1993, vol. 65, no1, pp. 316-324 (42 ref.);Cellular motions and thermal fluctuations : the Brownian ratchet) (ISSN 0006-3495).
- Paul Langevin, « Sur la théorie du mouvement brownien », Comptes-rendus de l'Académie des Sciences 146 (1908), 530-532. Lire en ligne sur Gallica.
- Cf. e.g. : Mark Kac ; Integration in Function Space and some of Its Applications, Lezioni Fermiane, Accademia Nazionale dei Lincei, Scuola Normale Superiore, Pisa, Italy (1980). Texte au format pdf.
Bibliographie
Aspects historiques- Jean Perrin, Mouvement brownien et réalité moléculaire, Annales de Chimie et de Physique 19 (8e série), (1909), 5-104. Possibilité de consulter et de télécharger le texte complet au format pdf depuis le site Gallica de la BNF.
- Jean Perrin, Les Atomes, Paris, Félix Alcan, 1913
- Albert Einstein, Investigations on the Theory of the Brownian Movement, Dover Publications, Inc. (1985), (ISBN 0-486-60304-0). Réédition des articles originaux d’Einstein sur la théorie du mouvement brownien.
- Jean-Pierre Kahane, Le mouvement brownien - Un essai sur les origines de la théorie mathématique, Séminaires et Congrès de la SMF (1998), vol 3., p. 123-155
- Bertrand Duplantier ; Le mouvement brownien, Séminaire Poincaré : Einstein, 1905-2005 (Paris, 8 avril 2005). Texte complet disponible ici.
- Bernard Derrida et Eric Brunet, Le mouvement brownien et le théorème de fluctuation-dissipation, dans : Michèle Leduc & Michel Le Bellac (éditeurs) ; Einstein aujourd'hui, EDP Sciences (janvier 2005), (ISBN 2-86883-768-9).
- Jean-François Le Gall, Mouvement brownien, martingales et calcul stochastique, Springer, 2013
- Jean-François Le Gall, Intégration, Probabilités et Processus Aléatoires, cours du Magistère de mathématiques de l'ENS (2005). Le dernier chapitre (14) est une introduction au mouvement brownien. Format pdf.
- Jean-François Le Gall, Mouvement brownien et calcul stochastique, cours de DEA donné à l'université Paris 6 (1996 et 1997). Format pdf.
- Jean-François Le Gall, Mouvement brownien, processus de branchement et superprocessus, cours de DEA donné à l'université Paris 6 (1994). Format pdf.
- Paul Lévy, Processus stochastiques et mouvement brownien, Gauthier-Villars (2e édition - 1965). Réédité par Jacques Gabay (1992), (ISBN 2-87647-091-8).
- Mark Kac, Random Walk and the Theory of Brownian Motion, American Mathematical Monthly 54(7) (1947), 369-391. Texte au format pdf.
- Mark Kac, Integration in Function Space and some of Its Applications, Lezioni Fermiane, Accademia Nazionale dei Lincei, Scuola Normale Superiore, Pisa, Italy (1980). Texte au format pdf.
- Edward Nelson, Dynamical Theories of Brownian Motion, Princeton University Press (1967). Texte au format pdf.
- Daniel Revuz et Marc Yor, Continuous martingales and Brownian motion, 3e ed., New York Springer (1999) (ISBN 3-540-64325-7).
- Elton P. Hsu ; Stochastic Analysis on Manifolds, American Mathematical Society (janvier 2002), (ISBN 0-8218-0802-8).
- Elton P. Hsu ; A Brief Introduction to Brownian Motion on a Riemannian Manifold, (2003). Cours donné à Kyoto, disponible au format pdf.
- Mark A. Pinsky ; Isotropic transport process on a Riemannian manifold, Transaction of the American Mathematical Society 218 (1976), 353-360.
- Mark A. Pinsky ; Can You Feel the Shape of a Manifold with Brownian Motion ?, Expositiones Mathematicae 2 (1984), 263-271.
- Nicolas Th. Varopoulos ; Brownian motion and random walks on manifolds, Annales de l'Institut Fourier 34(2) (1984), 243-269. Texte disponible au format pdf.
- Alexander Grigor'yan ; Analytic and geometric background of recurrence and non-explosion of the Brownian motion on Riemannian manifolds, Bulletin of the American Mathematical Society 36(2) (1999), 135-249. Texte en ligne.
Articles connexes
- Diffusion
- Migration (matière)
- Marche aléatoire
- Équation de Fokker-Planck
- Équation de la chaleur
- Feuille brownienne
- Noyau de la chaleur
- Processus stochastique
- Chaîne de Markov
- Intégrale de chemin
- Calcul stochastique
- Pont brownien
- Théorème de Donsker
- Projecteur (physique statistique)
- Physique statistique hors d'équilibre
- Hasard
- Thermodynamique
Liens externes
- (en) Article de blog sur le mouvement brownien
- (fr) Thermogramme du mouvement brownien visible en surface d'un bol d'eau chaude
 : si x(t) est la distance de la particule à sa position de départ à l'instant t, alors :
: si x(t) est la distance de la particule à sa position de départ à l'instant t, alors :


 est un mouvement brownien si et seulement si
(
M
t
)
{\displaystyle (M_{t})}
est un mouvement brownien si et seulement si
(
M
t
)
{\displaystyle (M_{t})}
 est une martingale.
est une martingale.
 est un
est un  est indépendant du processus
(
B
u
)
0
≤
u
≤
s
{\displaystyle (B_{u})_{0\leq u\leq s}}
est indépendant du processus
(
B
u
)
0
≤
u
≤
s
{\displaystyle (B_{u})_{0\leq u\leq s}}
 avant le temps s.
avant le temps s. est continue.
est continue. . On dit alors que le mouvement brownien est standard.
. On dit alors que le mouvement brownien est standard. , le vecteur
(
B
t
1
,
B
t
2
,
.
.
.
,
B
t
n
)
{\displaystyle (B_{t_{1}},B_{t_{2}},...,B_{t_{n}})}
, le vecteur
(
B
t
1
,
B
t
2
,
.
.
.
,
B
t
n
)
{\displaystyle (B_{t_{1}},B_{t_{2}},...,B_{t_{n}})}
 est un
est un  et la covariance est
E
=
min
(
s
,
t
)
{\displaystyle \mathbb {E} =\min(s,t)}
et la covariance est
E
=
min
(
s
,
t
)
{\displaystyle \mathbb {E} =\min(s,t)}
 .
. où les processus
B
1
,
B
2
,
.
.
.
,
B
d
{\displaystyle B^{1},B^{2},...,B^{d}}
où les processus
B
1
,
B
2
,
.
.
.
,
B
d
{\displaystyle B^{1},B^{2},...,B^{d}}
 sont des mouvements browniens indépendants.
sont des mouvements browniens indépendants.
 et ses projections sur les espaces
R
,
R
2
,
.
.
.
,
R
d
−
1
{\displaystyle \mathbb {R} ,\mathbb {R} ^{2},...,\mathbb {R} ^{d-1}}
et ses projections sur les espaces
R
,
R
2
,
.
.
.
,
R
d
−
1
{\displaystyle \mathbb {R} ,\mathbb {R} ^{2},...,\mathbb {R} ^{d-1}}
 sont respectivement des mouvements browniens uni-, bi-, ..., d-1-dimensionnels.
sont respectivement des mouvements browniens uni-, bi-, ..., d-1-dimensionnels.
 l'espace des fonctions continues de
R
+
{\displaystyle \mathbb {R} ^{+}}
l'espace des fonctions continues de
R
+
{\displaystyle \mathbb {R} ^{+}}
 dans
R
{\displaystyle \mathbb {R} }
dans
R
{\displaystyle \mathbb {R} }
 et
(
Ω
,
T
,
P
)
{\displaystyle (\Omega ,{\mathcal {T}},\mathbb {P} )}
et
(
Ω
,
T
,
P
)
{\displaystyle (\Omega ,{\mathcal {T}},\mathbb {P} )}
 un
un  .
.
 , est la mesure-image de
P
(
d
ω
)
{\displaystyle \mathbb {P} (\mathrm {d} \omega )}
, est la mesure-image de
P
(
d
ω
)
{\displaystyle \mathbb {P} (\mathrm {d} \omega )}
 par cette application B.
par cette application B.
 ,
,
 .
.
 sont des
sont des  , la fonction
t
↦
B
t
(
ω
)
{\displaystyle t\mapsto B_{t}(\omega )}
, la fonction
t
↦
B
t
(
ω
)
{\displaystyle t\mapsto B_{t}(\omega )}
 , le processus
(
B
t
T
)
t
≥
0
:=
(
B
T
+
t
−
B
T
)
t
≥
0
{\displaystyle (B_{t}^{T})_{t\geq 0}:=(B_{T+t}-B_{T})_{t\geq 0}}
, le processus
(
B
t
T
)
t
≥
0
:=
(
B
T
+
t
−
B
T
)
t
≥
0
{\displaystyle (B_{t}^{T})_{t\geq 0}:=(B_{T+t}-B_{T})_{t\geq 0}}
 est un mouvement brownien indépendant du processus
(
B
s
)
0
≤
s
<
T
{\displaystyle (B_{s})_{0\leq s<T}}
est un mouvement brownien indépendant du processus
(
B
s
)
0
≤
s
<
T
{\displaystyle (B_{s})_{0\leq s<T}}
 .
. . On retrouve le fait que le mouvement brownien soit un processus de Lévy sans drift (« dérive »), sans sauts et de coefficient quadratique 1/2.
. On retrouve le fait que le mouvement brownien soit un processus de Lévy sans drift (« dérive »), sans sauts et de coefficient quadratique 1/2. est un mouvement brownien indépendant de
(
B
u
)
0
≤
u
≤
s
{\displaystyle (B_{u})_{0\leq u\leq s}}
est un mouvement brownien indépendant de
(
B
u
)
0
≤
u
≤
s
{\displaystyle (B_{u})_{0\leq u\leq s}}
 est un mouvement brownien. On dit que le mouvement brownien est stable d'indice 2.
est un mouvement brownien. On dit que le mouvement brownien est stable d'indice 2. qui s'annule en t=0 est un mouvement brownien.
qui s'annule en t=0 est un mouvement brownien. , l'ensemble
{
t
≥
0
,
|
|
B
t
−
x
|
|
≤
r
}
{\displaystyle \{t\geq 0,||B_{t}-x||\leq r\}}
, l'ensemble
{
t
≥
0
,
|
|
B
t
−
x
|
|
≤
r
}
{\displaystyle \{t\geq 0,||B_{t}-x||\leq r\}}
 est non borné pour tout
x
∈
R
d
{\displaystyle x\in \mathbb {R} ^{d}}
est non borné pour tout
x
∈
R
d
{\displaystyle x\in \mathbb {R} ^{d}}
 et tout
r
⪈
0
{\displaystyle r\gneq 0}
et tout
r
⪈
0
{\displaystyle r\gneq 0}
 ,
si
d
≥
3
,
lim
t
→
∞
‖
B
t
‖
=
+
∞
{\displaystyle d\geq 3,\,\,\,\lim _{t\rightarrow \infty }\|B_{t}\|=+\infty }
,
si
d
≥
3
,
lim
t
→
∞
‖
B
t
‖
=
+
∞
{\displaystyle d\geq 3,\,\,\,\lim _{t\rightarrow \infty }\|B_{t}\|=+\infty }
 presque sûrement.
presque sûrement.

 une famille de fonctions à valeurs réelles appartenant à
L
2
(
R
+
)
{\displaystyle L^{2}(\mathbb {R} _{+})}
une famille de fonctions à valeurs réelles appartenant à
L
2
(
R
+
)
{\displaystyle L^{2}(\mathbb {R} _{+})}
 . Posons alors :
. Posons alors :

 et tous
t
1
,
.
.
.
,
t
k
∈
R
+
{\displaystyle t_{1},...,t_{k}\in \mathbb {R} _{+}}
et tous
t
1
,
.
.
.
,
t
k
∈
R
+
{\displaystyle t_{1},...,t_{k}\in \mathbb {R} _{+}}
 , la matrice
(
s
(
t
i
,
t
j
)
)
1
≤
i
,
j
≤
k
{\displaystyle \left(s(t_{i},t_{j})\right)_{1\leq i,j\leq k}}
, la matrice
(
s
(
t
i
,
t
j
)
)
1
≤
i
,
j
≤
k
{\displaystyle \left(s(t_{i},t_{j})\right)_{1\leq i,j\leq k}}
 est symétrique et semi-définie positive.
est symétrique et semi-définie positive.
 dont la fonction moyenne m est arbitraire et dont la fonction de covariance est s définie au-dessus.
dont la fonction moyenne m est arbitraire et dont la fonction de covariance est s définie au-dessus.
 où
c
>
0
{\displaystyle c>0}
où
c
>
0
{\displaystyle c>0}
 est une constante ne dépendant pas de t, et où
1
1
{\displaystyle 1\!\!1_{}}
est une constante ne dépendant pas de t, et où
1
1
{\displaystyle 1\!\!1_{}}
 est la fonction indicatrice sur , il résulte de l'expression de s que pour tout
(
u
,
v
)
∈
R
+
2
{\displaystyle (u,v)\in {\mathbb {R} _{+}^{2}}}
est la fonction indicatrice sur , il résulte de l'expression de s que pour tout
(
u
,
v
)
∈
R
+
2
{\displaystyle (u,v)\in {\mathbb {R} _{+}^{2}}}
 :
:

 et
t
1
,
.
.
.
,
t
k
{\displaystyle t_{1},...,t_{k}}
et
t
1
,
.
.
.
,
t
k
{\displaystyle t_{1},...,t_{k}}
 2 à 2 distincts.
2 à 2 distincts.
 est un mouvement brownien lorsque le processus est centré (i.e. l'application
t
↦
E
X
t
{\displaystyle t\mapsto \mathbb {E} X_{t}}
est un mouvement brownien lorsque le processus est centré (i.e. l'application
t
↦
E
X
t
{\displaystyle t\mapsto \mathbb {E} X_{t}}
 est identiquement nulle) et que sa fonction de covariance s est donnée ci-dessus. D'habitude, un mouvement brownien est noté par
{
B
t
}
t
∈
R
+
{\displaystyle \{B_{t}\}_{t\in \mathbb {R} _{+}}}
est identiquement nulle) et que sa fonction de covariance s est donnée ci-dessus. D'habitude, un mouvement brownien est noté par
{
B
t
}
t
∈
R
+
{\displaystyle \{B_{t}\}_{t\in \mathbb {R} _{+}}}
 .
Signalons que
c
=
Var
(
B
1
)
{\displaystyle c=\operatorname {Var} (B_{1})}
.
Signalons que
c
=
Var
(
B
1
)
{\displaystyle c=\operatorname {Var} (B_{1})}
 . Lorsque c = 1, le mouvement brownien est dit standard.
. Lorsque c = 1, le mouvement brownien est dit standard.

 2. La convergence
⟶
n
→
∞
{\displaystyle {\underset {n\rightarrow \infty }{\longrightarrow }}}
2. La convergence
⟶
n
→
∞
{\displaystyle {\underset {n\rightarrow \infty }{\longrightarrow }}}
 est la
est la  et
(
N
k
′
,
k
∈
N
)
{\displaystyle (N'_{k},k\in \mathbb {N} )}
et
(
N
k
′
,
k
∈
N
)
{\displaystyle (N'_{k},k\in \mathbb {N} )}
 de variables aléatoires indépendantes de
de variables aléatoires indépendantes de  . Le processus
(
B
t
)
t
≥
0
{\displaystyle (B_{t})_{t\geq 0}}
. Le processus
(
B
t
)
t
≥
0
{\displaystyle (B_{t})_{t\geq 0}}

 l'ensemble des zéros du mouvement brownien unidimensionnel (ensemble des temps où le mouvement brownien s'annule). Le complémentaire de
B
{\displaystyle {\mathcal {B}}}
l'ensemble des zéros du mouvement brownien unidimensionnel (ensemble des temps où le mouvement brownien s'annule). Le complémentaire de
B
{\displaystyle {\mathcal {B}}}
 est une suite d'intervalles ouverts que l'on note
⋃
n
≥
1
B
n
{\displaystyle \bigcup _{n\geq 1}{\mathcal {B}}_{n}}
est une suite d'intervalles ouverts que l'on note
⋃
n
≥
1
B
n
{\displaystyle \bigcup _{n\geq 1}{\mathcal {B}}_{n}}
 . Chaque intervalle a une longueur notée
|
B
n
|
{\displaystyle |{\mathcal {B}}_{n}|}
. Chaque intervalle a une longueur notée
|
B
n
|
{\displaystyle |{\mathcal {B}}_{n}|}
 .
.
 et
e
n
n
o
r
m
:=
(
e
n
n
o
r
m
(
t
)
,
0
≤
t
≤
1
)
{\displaystyle e_{n}^{norm}:=(e_{n}^{norm}(t),0\leq t\leq 1)}
et
e
n
n
o
r
m
:=
(
e
n
n
o
r
m
(
t
)
,
0
≤
t
≤
1
)
{\displaystyle e_{n}^{norm}:=(e_{n}^{norm}(t),0\leq t\leq 1)}
 par
par
 pour tout
0
≤
t
≤
|
B
n
|
{\displaystyle 0\leq t\leq |{\mathcal {B}}_{n}|}
pour tout
0
≤
t
≤
|
B
n
|
{\displaystyle 0\leq t\leq |{\mathcal {B}}_{n}|}
 ,
e
n
n
o
r
m
(
t
)
:=
B
t
|
B
n
|
+
inf
B
n
|
B
n
|
{\displaystyle e_{n}^{norm}(t):={\frac {B_{t|{\mathcal {B}}_{n}|+\inf {\mathcal {B}}_{n}}}{\sqrt {|{\mathcal {B}}_{n}|}}}}
,
e
n
n
o
r
m
(
t
)
:=
B
t
|
B
n
|
+
inf
B
n
|
B
n
|
{\displaystyle e_{n}^{norm}(t):={\frac {B_{t|{\mathcal {B}}_{n}|+\inf {\mathcal {B}}_{n}}}{\sqrt {|{\mathcal {B}}_{n}|}}}}
 pour tout
0
≤
t
≤
1
{\displaystyle 0\leq t\leq 1}
pour tout
0
≤
t
≤
1
{\displaystyle 0\leq t\leq 1}
 .
.
 est appelée l'
est appelée l' est l'excursion brownienne normalisée (voir le livre de Itô et McKean
est l'excursion brownienne normalisée (voir le livre de Itô et McKean ) soit "au-dessous" de 0 (s'il existe un t tel que
e
n
(
t
)
<
0
{\displaystyle e_{n}(t)<0}
) soit "au-dessous" de 0 (s'il existe un t tel que
e
n
(
t
)
<
0
{\displaystyle e_{n}(t)<0}
 ).
).
 sont indépendantes et de même loi. De même pour
(
e
n
n
o
r
m
,
n
≥
1
)
{\displaystyle (e_{n}^{norm},n\geq 1)}
sont indépendantes et de même loi. De même pour
(
e
n
n
o
r
m
,
n
≥
1
)
{\displaystyle (e_{n}^{norm},n\geq 1)}
 .
e
1
n
o
r
m
{\displaystyle e_{1}^{norm}}
.
e
1
n
o
r
m
{\displaystyle e_{1}^{norm}}
 est markovien avec :
est markovien avec : .
.
 .
.
 est soumise à deux forces :
est soumise à deux forces :
 , où k est une constante positive ;
, où k est une constante positive ;


 est une constante positive, et
δ
(
t
)
{\displaystyle \delta (t)}
est une constante positive, et
δ
(
t
)
{\displaystyle \delta (t)}
 est la
est la 
 est la dérivée de
η
{\displaystyle \eta }
est la dérivée de
η
{\displaystyle \eta }
 par rapport au temps t.
par rapport au temps t.

 de l'équation différentielle stochastique suivante :
d
X
t
=
2
d
B
t
−
X
t
d
t
{\displaystyle dX_{t}={\sqrt {2}}dB_{t}-X_{t}dt}
de l'équation différentielle stochastique suivante :
d
X
t
=
2
d
B
t
−
X
t
d
t
{\displaystyle dX_{t}={\sqrt {2}}dB_{t}-X_{t}dt}
 ,
où
B
t
{\displaystyle B_{t}}
,
où
B
t
{\displaystyle B_{t}}
 est un mouvement brownien standard,
et avec
X
0
{\displaystyle X_{0}}
est un mouvement brownien standard,
et avec
X
0
{\displaystyle X_{0}}
 une variable aléatoire donnée.
Le terme
d
B
t
{\displaystyle dB_{t}}
une variable aléatoire donnée.
Le terme
d
B
t
{\displaystyle dB_{t}}
 traduit les nombreux chocs aléatoires subis par la particule,
alors que le terme
−
X
t
d
t
{\displaystyle -{X_{t}}dt}
traduit les nombreux chocs aléatoires subis par la particule,
alors que le terme
−
X
t
d
t
{\displaystyle -{X_{t}}dt}
 représente la force de frottement subie par la particule.
représente la force de frottement subie par la particule.
 nous donne :
d
(
e
t
X
t
)
=
e
t
X
t
d
t
+
e
t
(
2
d
B
t
−
X
t
d
t
)
=
e
t
2
d
B
t
{\displaystyle d({e^{t}}X_{t})={e^{t}}{X_{t}}dt+{e^{t}}({\sqrt {2}}{dB_{t}}-{X_{t}}dt)={e^{t}}{\sqrt {2}}{dB_{t}}}
nous donne :
d
(
e
t
X
t
)
=
e
t
X
t
d
t
+
e
t
(
2
d
B
t
−
X
t
d
t
)
=
e
t
2
d
B
t
{\displaystyle d({e^{t}}X_{t})={e^{t}}{X_{t}}dt+{e^{t}}({\sqrt {2}}{dB_{t}}-{X_{t}}dt)={e^{t}}{\sqrt {2}}{dB_{t}}}
 ,
soit, sous forme intégrale :
X
t
=
X
0
e
−
t
+
2
e
−
t
∫
0
t
e
s
d
B
s
{\displaystyle X_{t}={X_{0}}e^{-t}+{\sqrt {2}}e^{-t}\int _{0}^{t}{e^{s}}dB_{s}}
,
soit, sous forme intégrale :
X
t
=
X
0
e
−
t
+
2
e
−
t
∫
0
t
e
s
d
B
s
{\displaystyle X_{t}={X_{0}}e^{-t}+{\sqrt {2}}e^{-t}\int _{0}^{t}{e^{s}}dB_{s}}

 ,
la loi de
X
t
{\displaystyle X_{t}}
,
la loi de
X
t
{\displaystyle X_{t}}
 et de variance
1
−
e
−
2
t
{\displaystyle 1-e^{-2t}}
et de variance
1
−
e
−
2
t
{\displaystyle 1-e^{-2t}}
 ,
ce qui converge en loi quand
t
{\displaystyle t}
,
ce qui converge en loi quand
t
{\displaystyle t}
 tend vers l'infini vers la loi gaussienne centrée réduite.
tend vers l'infini vers la loi gaussienne centrée réduite.

 de maille a sur l'axe, chaque saut ayant une durée
τ
{\displaystyle \tau }
de maille a sur l'axe, chaque saut ayant une durée
τ
{\displaystyle \tau }
 .
.


 sachant qu'elle était au site na à l'instant initial 0.
sachant qu'elle était au site na à l'instant initial 0.




 doit en fait rester constante dans cette limite continue.
doit en fait rester constante dans cette limite continue.






 doit vérifier les deux conditions supplémentaires suivantes :
doit vérifier les deux conditions supplémentaires suivantes :


 est la
est la 
 pour simplifier. La densité de probabilité de transition conditionnelle
P
0
(
x
,
t
)
=
P
(
0
|
x
,
t
)
{\displaystyle P_{0}(x,t)=P(0|x,t)}
pour simplifier. La densité de probabilité de transition conditionnelle
P
0
(
x
,
t
)
=
P
(
0
|
x
,
t
)
{\displaystyle P_{0}(x,t)=P(0|x,t)}
 permet le calcul des divers moments :
permet le calcul des divers moments :

 étant paire, tous les moments d'ordre impair sont nuls. On peut facilement calculer tous les moments d'ordre pair en posant :
étant paire, tous les moments d'ordre impair sont nuls. On peut facilement calculer tous les moments d'ordre pair en posant :




 , où
Δ
V
{\displaystyle \Delta _{V}}
, où
Δ
V
{\displaystyle \Delta _{V}}
 est l'
est l'