Polyèdre régulier
Dans le monde d'aujourd'hui, Polyèdre régulier est devenu une question pertinente qui a un impact significatif sur différents domaines de la société. Avec l'augmentation de la mondialisation et l'interconnexion entre les cultures, Polyèdre régulier a acquis une pertinence croissante, générant des débats et des réflexions qui transcendent les frontières et les disciplines. Dans cet article, nous explorerons les différentes facettes de Polyèdre régulier, en analysant son impact aujourd'hui et en réfléchissant à son influence dans le futur. Dans une perspective large et interdisciplinaire, nous approfondirons les aspects historiques, sociaux, politiques et culturels de Polyèdre régulier, dans le but de comprendre sa complexité et ses implications dans le monde contemporain.
Un polyèdre est dit régulier s'il est constitué de faces toutes identiques et régulières, et que tous ses sommets sont identiques (qu'il y a un même nombre d'arêtes qui convergent à chaque sommet).
Il existe cinq polyèdres réguliers convexes, connus sous le nom de solides de Platon.
Il existe quatre polyèdres réguliers non convexes, connus sous le nom de solides de Kepler-Poinsot.
Solides de Platon
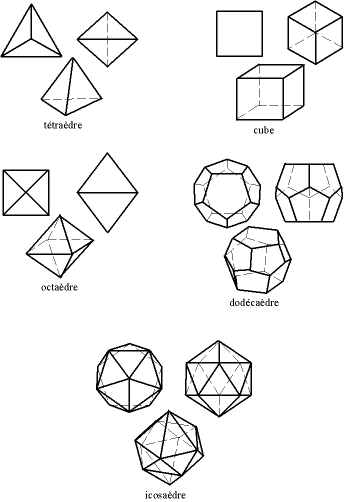
Il semble que Pythagore lui-même (vers 530 av. J.-C.) ou le pythagoricien Archytas de Tarente (vers 360 av. J.-C.), ait découvert les trois premiers des cinq : le tétraèdre (la pyramide), l'hexaèdre (le cube), le dodécaèdre. Ensuite, Théétète d'Athènes (mort en 395 ou en 369 av. J.-C.) découvrit les deux autres : l'octaèdre et l'icosaèdre. Platon les utilise profondément dans le Timée (54 e - 56 c), qui date de 358 av. J.-C. Euclide les étudie dans ses Éléments (vers 300 av. J.-C.)
Le tétraèdre régulier (pyramide)
Le tétraèdre régulier (de tétra, quatre, et èdre, base), polyèdre à 4 faces triangulaires,
- est constitué de 4 faces en triangle équilatéral,
- possède 4 sommets et 6 arêtes.
L'hexaèdre régulier (cube)
L'hexaèdre (de hexa, six, et èdre, base)
- est constitué de 6 faces carrées,
- possède 8 sommets et 12 arêtes,
- possède 24 triangles rectangles isocèles.
L'octaèdre régulier
L'octaèdre (de octa, huit, et èdre, base)
- est constitué de 8 faces en triangle équilatéral,
- possède 6 sommets et 12 arêtes,
- possède 48 triangles rectangles scalènes.
Le dodécaèdre régulier
Le dodécaèdre (de dodéca, douze, et èdre, base)
- est constitué de 12 faces pentagonales égales,
- possède 20 sommets et 30 arêtes.
L'icosaèdre
L'icosaèdre (de icosa, vingt, et èdre, base)
- est constitué de 20 faces en triangle équilatéral,
- possède 12 sommets et 30 arêtes,
- possède 120 triangles rectangles scalènes.
Les centres des faces d'un solide de Platon sont les sommets d'un solide de Platon. Cette correspondance est interne parmi les tétraèdres ; elle échange cubes et octaèdres d'une part, dodécaèdres et icosaèdres d'autre part.
Platon considérait ces solides comme l'image de la perfection ; pour lui, comme il l'explique dans le Timée, le tétraèdre est le symbole du feu, l'octaèdre celui de l'air, l'icosaèdre celui de l'eau, le cube celui de la terre et le dodécaèdre celui de l'univers tout entier.
Deux mémoires de Cauchy au Journal de l'École polytechnique[1] traitent des polyèdres réguliers.
Les mathématiques classiques rattachent ces cinq solides réguliers à la notion de groupe.
Démonstration
On va montrer qu'il ne peut exister que les cinq polyèdres réguliers convexes de Platon ; cette démonstration est équivalente à celle d'Euclide.
Conditions
Soient m le nombre d'arêtes d'une face, n le nombre de faces qui se rejoignent en un sommet du polyèdre ({m,n} est le symbole de Schläfli du polyèdre). Nous savons que :
- m et n sont des nombres entiers naturels ;
- m ≥ 3, car un polygone, figure en deux dimensions, possède au moins trois arêtes ;
- n ≥ 3, car un sommet dans un polyèdre, figure en trois dimensions, ne peut rejoindre moins de trois faces ;
- l'angle d'un m-polygone régulier vaut degrés : 60 degrés pour un triangle équilatéral, 90 pour un carré, 108 pour un pentagone régulier, 120 pour un hexagone régulier, etc. ;
- la somme s des angles en un sommet est strictement inférieure à 360 degrés, sans quoi les faces sont coplanaires (s = 360 degrés) ou se chevauchent (s > 360 degrés).
Équation
Il s'agit donc de trouver toutes les solutions du système suivant :
Solutions
- Si m = 3 (faces triangulaires), alors les valeurs qui conviennent sont :
- n = 3, car s(3,3) = 180 < 360 : c'est le tétraèdre
- n = 4, car s(3,4) = 240 < 360 : c'est l'octaèdre
- n = 5, car s(3,5) = 300 < 360 : c'est l'icosaèdre
- Si n ≥ 6, alors le résultat est trop grand : s(3,6) = 360. On retrouve en effet six triangles équilatéraux ayant un sommet commun, formant donc un hexagone régulier plat.
- Si m = 4 (faces carrées), la seule solution est :
- n = 3, car s(4,3) = 270 < 360 : c'est le cube
- Si n ≥ 4, alors le résultat est trop grand : s(4,4) = 360. On retrouve en effet quatre carrés ayant un sommet commun, formant donc un carré plat.
- Si m = 5 (faces pentagonales) :
- n = 3, car s(5,3) = 324 < 360 : c'est le dodécaèdre.
- Si n ≥ 4, alors le résultat est trop grand : s(5,4) = 432 > 360.
Si m ≥ 6, il n'y a plus de solution : s(6,3) = 360 et si m ≥ 6 alors s(m,n) = > 360 pour tout n ≥ 3.
Dualité
Cette méthode permet d'identifier également les polyèdres duaux, car il suffit d'inverser m et n pour obtenir le dual d'un polyèdre :
- le dual du tétraèdre {3,3} est le tétraèdre {3,3} lui-même ;
- le dual de l'octaèdre {3,4} est le cube {4,3} ;
- le dual de l'icosaèdre {3,5} est le dodécaèdre {5,3}.
On voit également que le tétraèdre est le seul autodual, car, une fois posé m = n, la seule solution entière de l'équation
est n = 3, puisque s(3,3) = 180 < 360 ; alors qu'avec n = 4, le résultat est trop grand : s(4,4) = 360.
Les polyèdres de Kepler-Poinsot
Outre les cinq solides de Platon, on peut construire quatre autres solides réguliers, deux dont les faces sont des polygones réguliers étoilés (ou croisés) : les solides de Kepler, et deux ayant des faces régulières, mais qui peuvent s'interpénétrer : les solides de Poinsot.

- Le petit dodécaèdre étoilé a été découvert par Kepler vingt-deux siècles après Platon, en 1619. Il a 12 faces qui sont des pentagones étoilés, 12 sommets et 30 arêtes. En chaque sommet se réunissent cinq faces. Ce petit dodécaèdre étoilé peut être vu dans une mosaïque de Paolo Uccello, dans la basilique Saint-Marc de Venise, réalisée approximativement en 1430 (soit près de 200 ans avant sa description mathématique).
- Le grand dodécaèdre étoilé, découvert par Kepler, formé des mêmes 12 pentagones étoilés, qui a 20 sommets et aussi 30 arêtes.
- Le grand dodécaèdre découvert par Poinsot en 1809. Ses 12 faces sont des pentagones réguliers, il a 12 sommets et 30 arêtes. Plus de 200 ans auparavant, dans sa Perspectiva corporum regularium (« Perspectives des solides réguliers »)[2], un livre de gravures sur bois publié en 1568, Wenzel Jamnitzer dépeint le grand dodécaèdre.
- Le grand icosaèdre, découvert par Poinsot, formé de 20 triangles équilatéraux, et qui possède 12 sommets et aussi 30 arêtes.
-
Petit dodécaèdre étoilé {5/2, 5}.
-
Grand dodécaèdre étoilé {5/2, 3}.
-
Grand dodécaèdre {3, 5/2}.
-
Grand icosaèdre {5, 5/2}.
Notes et références
Articles connexes
- Les dômes géodésiques ou géodes
- Les polychores réguliers sont les analogues à 4 dimensions des polyèdres réguliers.






