Logarithme népérien
Fonction logarithme népérien ou naturel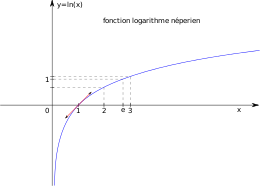
Courbe représentative de la fonction
x
↦
ln
x
{\displaystyle x\mapsto \ln x}
.
.| Notation | ln {\displaystyle \ln } |
|---|---|
| Réciproque | exp {\displaystyle \exp } |
| Dérivée | x ↦ 1 x {\displaystyle x\mapsto {\frac {1}{x}}} |
| Primitives | x ↦ x ln x − x + C {\displaystyle x\mapsto x\ln x-x+C} |
| Ensemble de définition | R + ∗ {\displaystyle \mathbb {R} _{+}^{*}} |
|---|---|
| Ensemble image | R {\displaystyle \mathbb {R} } |
| Limite en +∞ | +∞ |
|---|
| Asymptotes | x = 0 {\displaystyle x=0} |
|---|---|
| Zéros | 1 |
Le logarithme népérien, ou logarithme naturel, ou encore jusqu'au XXe siècle logarithme hyperbolique, transforme, comme les autres fonctions logarithmes, les produits en sommes. L'utilisation de telles fonctions permet de faciliter les calculs comprenant de nombreuses multiplications, divisions et élévations à des puissances rationnelles. Il est souvent noté ln().
Le logarithme naturel ou népérien est dit de base e car ln(e) = 1.
Le logarithme népérien d'un nombre x peut également être défini comme la puissance à laquelle il faut élever e pour obtenir x. La fonction logarithme népérien est donc la bijection réciproque de la fonction exponentielle. C'est également la primitive définie sur les réels strictement positifs et qui s'annule en 1 de la fonction inverse x ↦ 1/x.
Cette fonction fut notée l. ou l, dès le début du XVIIIe siècle, et jusque dans la première moitié du XIXe siècle, puis log. ou log dès la fin du XVIIIe siècle, puis Log pour la différencier de la fonction log (logarithme de base quelconque, ou plus particulièrement logarithme décimal), ou encore logh (« logarithme hyperbolique »), avant que ne tente de s'imposer la notation préconisée par les normes AFNOR de 1961 et ISO 80000-2 : la notation ln. Avec un succès cependant très relatif : la notation log est encore aujourd'hui utilisée dans plusieurs branches des mathématiques, et tout particulièrement en théorie des nombres, ainsi que dans plusieurs langages de programmation, comme C, C++, SAS, R, MATLAB, Mathematica, Fortran, et BASIC.
Historique
Article connexe : Histoire des logarithmes et des exponentielles.
Table des logarithmes naturels de 0,01 à 100 avec cinq chiffres après la virgule.
Ce logarithme est appelé népérien, en hommage au mathématicien écossais John Napier qui établit les premières tables logarithmiques (lesquelles ne sont en fait pas des tables de logarithmes népériens). On date en général l'origine des logarithmes népériens en 1647, lorsque Grégoire de Saint-Vincent travaille sur la quadrature de l'hyperbole et démontre que la fonction obtenue vérifie la propriété d'additivité des fonctions logarithmes. Saint-Vincent ne voit cependant pas de lien avec les logarithmes de Napier, et c'est son disciple Alphonse Antoine de Sarasa qui l'expliquera en 1649. Le logarithme népérien s'est tout d'abord appelé « logarithme hyperbolique », en référence à l'aire sous l'hyperbole qu'il représente. L'appelation « logarithme naturel », due à Pietro Mengoli en 1659, est reprise en 1668 dans une note de Nicolaus Mercator sur la série qui porte son nom. Cette série, exploitée par Newton en 1671, permet de calculer assez simplement les valeurs du logarithme de Grégoire de Saint-Vincent. Le calcul des autres logarithmes apparaît alors bien compliqué et, naturellement, celui de Grégoire de Saint-Vincent devient alors le logarithme le plus naturel.
Pour tout réel a > 0, ln(a) peut être défini comme l'aire du domaine délimité par la courbe représentative de la fonction x↦1/x, l'axe des abscisses et les droites d'abscisses 1 et a.
La fonction logarithme naturel comme primitive de la fonction inverse
La fonction x ↦ 1/x est continue sur ]0, +∞0, +∞0, +∞0, +∞0, +∞0, +∞0, +∞0, +∞ 0 , + ∞ 0,+\infty 0,+\infty − 1 , 1 -1,1\right-1,1\right ou le théorème de convergence radiale d'Abel, ce développement est encore valide pour x = 1. On obtient ainsi la somme de la série harmonique alternée.
D'autre part, notons que Leonhard Euler a hardiment appliqué ce développement à x = –1. Sans se soucier de la convergence, il montre que la série harmonique est le logarithme naturel de 1/1 – 1, c'est-à-dire de l'infini. Aujourd'hui on formalise cette remarque d'Euler par : « la série harmonique tronquée en N est proche du logarithme de N lorsque N est grand » ; plus précisément, les différences entre somme partielle de la série harmonique et logarithme naturel convergent vers la constante d'Euler-Mascheroni.
Pour obtenir une meilleure vitesse de convergence, on peut en déduire :
∀ x ∈ ] − 1 , 1 -1,1\right-1,1\right 0 , + ∞ 0,+\infty \right0,+\infty \right0, +∞0, +∞ (6e éd., Oxford, 2008, 1.7) « log x is, of course the 'Napierian' logarithm of x, to base e. 'Common' logarithms have no mathematical interest. »Voir aussi
Articles connexes
- Exemple d'application du théorème de Gelfond-Schneider : ln(3)/ln(2) est transcendant
- Logarithme népérien de deux
- Logarithme binaire
- Logarithme discret
- Logarithme intégral
- Fonction W de Lambert
Liens externes
« Poser la modélisation comme question épistémologique pour l’introduction des propriétés des exponentielles dans les classes », conférence de Jean Dhombres : parties 1, 2 et 3
Une excellente vidéo en anglais expliquant l'origine des logarithmes naturels
