Théorème de factorisation

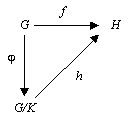Diagramme commutatif représentant les morphismes du théorème de factorisation

En mathématiques, le théorème de factorisation est un principe général qui permet de construire un morphisme d'une structure quotient X / R {\displaystyle X/R} $X/R$ dans un autre espace Y {\displaystyle Y} $Y$ à partir d'un morphisme de X {\displaystyle X} $X$ vers Y {\displaystyle Y} $Y$ , de façon à factoriser ce dernier par la surjection canonique de passage au quotient.

Le cas des ensembles

Soit X {\displaystyle X} $X$ un ensemble muni d'une relation d'équivalence R {\displaystyle R} $R$ et s : X → X / R {\displaystyle s:X\to X/R} $s:X\to X/R$ la surjection canonique.

Théorème — Soit f : X → Y {\displaystyle f:X\to Y} $f:X\to Y$ une application telle que (pour toute paire d'éléments x, x' dans X)

x R x ′ ⇒ f ( x ) = f ( x ′ ) {\displaystyle xRx'\Rightarrow f(x)=f(x')}

xRx'\Rightarrow f(x)=f(x')

Alors, il existe une unique application

g : X / R → Y telle que f = g ∘ s {\displaystyle g:X/R\to Y{\text{ telle que }}f=g\circ s}

g:X/R\to Y{\text{ telle que }}f=g\circ s

De plus :

g {\displaystyle g} $g$ est injective si et seulement si, réciproquement, f ( x ) = f ( x ′ ) ⇒ x R x ′ {\displaystyle f(x)=f(x')\Rightarrow xRx'} $f(x)=f(x')\Rightarrow xRx'$ (et donc si f ( x ) = f ( x ′ ) ⇔ x R x ′ {\displaystyle f(x)=f(x')\Leftrightarrow xRx'} $f(x)=f(x')\Leftrightarrow xRx'$ ) ;
g {\displaystyle g} $g$ est surjective si et seulement si f {\displaystyle f} $f$ est surjective ;
g {\displaystyle g} $g$ est bijective si f {\displaystyle f} $f$ est surjective et si x R x ′ ⟺ f ( x ) = f ( x ′ ) {\displaystyle xRx'\Longleftrightarrow f(x)=f(x')} $xRx'\Longleftrightarrow f(x)=f(x')$ .

Démonstration

L'unicité de g est immédiate et guide la preuve de son existence, dont voici plusieurs variantes :
- Preuve « naïve » : pour tout élément z = s ( x ) ∈ X / R {\displaystyle z=s(x)\in X/R} $z=s(x)\in X/R$ , on pose g ( z ) = f ( x ) {\displaystyle g(z)=f(x)} $g(z)=f(x)$ . Si z = s ( x ′ ) {\displaystyle z=s(x')} $z=s(x')$ pour un élément x ′ {\displaystyle x'} $x'$ équivalent à x {\displaystyle x} $x$ , on a f ( x ) = f ( x ′ ) {\displaystyle f(x)=f(x')} $f(x)=f(x')$ par hypothèse. Donc g {\displaystyle g} $g$ est bien définie. Par construction, f = g∘s.
- Formalisation de la preuve « naïve », rendant plus manifeste l'utilisation de l'axiome du choix : soit t une section de s (c'est-à-dire une application qui à chaque classe associe un élément de cette classe). On pose g = f∘t. Alors, pour tout élément x de X, (t∘s)(x) R x donc f((t∘s)(x)) = f(x), c'est-à-dire (g∘s)(x) = f(x) ; on a donc bien f = g∘s.
- Preuve sans axiome du choix : par hypothèse, f envoie tous les éléments d'une classe z sur un même élément y de Y. L'assignation z ↦ y définit alors l'application g qui convient.
- Formalisation de la preuve sans axiome du choix : en notant F et S les graphes de f et s, la relation binaire G = F ∘ S−1 (définie par : zGy s'il existe un x tel que z = s(x) et f(x) = y) est fonctionnelle et définit l'application g qui convient.
Si f est surjective, l'égalité f = g∘s implique que g est aussi surjective.
Supposons que x R x ′ {\displaystyle xRx'} $xRx'$ est équivalent à f ( x ) = f ( x ′ ) {\displaystyle f(x)=f(x')} $f(x)=f(x')$ . Soient z 1 = s ( x 1 ) , z 2 = s ( x 2 ) {\displaystyle z_{1}=s(x_{1}),z_{2}=s(x_{2})} $z_{1}=s(x_{1}),z_{2}=s(x_{2})$ tels que g ( z 1 ) = g ( z 2 ) {\displaystyle g(z_{1})=g(z_{2})} $g(z_{1})=g(z_{2})$ . Alors f ( x 1 ) = f ( x 2 ) {\displaystyle f(x_{1})=f(x_{2})} $f(x_{1})=f(x_{2})$ , donc x 1 R x 2 {\displaystyle x_{1}Rx_{2}} $x_{1}Rx_{2}$ et z 1 = s ( x 1 ) = s ( x 2 ) = z 2 {\displaystyle z_{1}=s(x_{1})=s(x_{2})=z_{2}} $z_{1}=s(x_{1})=s(x_{2})=z_{2}$ . Ce qui veut dire que g {\displaystyle g} $g$ est injective.
La dernière propriété résulte des deux précédentes.

(La réciproque est moins utile mais immédiate : pour toute application g : X/R → Y, la composée f = g∘s vérifie x R x' ⇒ f(x) = f(x').)

Ce théorème peut se spécialiser à un certain nombre de structures algébriques ou topologiques.

Le cas des groupes

Article détaillé : Théorèmes d'isomorphisme.

Sur un groupe G {\displaystyle G} $G$ , on considère la relation d'équivalence définie par un sous-groupe normal H {\displaystyle H} $H$ de G {\displaystyle G} $G$ : x R x ′ {\displaystyle xRx'} $xRx'$ si x ∈ x ′ H {\displaystyle x\in x'H} $x\in x'H$ . Alors, la surjection canonique s : G → G / H = G / R {\displaystyle s:G\to G/H=G/R} $s:G\to G/H=G/R$ est un morphisme de groupes et le théorème de factorisation s'énonce

Théorème — Soit f : G → K {\displaystyle f:G\to K} $f:G\to K$ un morphisme de groupes. Si H {\displaystyle H} $H$ est contenu dans le noyau de f {\displaystyle f} $f$ , alors il existe un unique morphisme de groupes g : G / H → K {\displaystyle g:G/H\to K} $g:G/H\to K$ tel que f = g ∘ s {\displaystyle f=g\circ s} $f=g\circ s$ . De plus :

g {\displaystyle g} $g$ est surjectif si f {\displaystyle f} $f$ est surjectif ;
g {\displaystyle g} $g$ est injectif si on a H = ker ⁡ f {\displaystyle H=\ker f} $H=\ker f$ ;
g {\displaystyle g} $g$ est un isomorphisme si f {\displaystyle f} $f$ est surjectif et H = ker ⁡ f {\displaystyle H=\ker f} $H=\ker f$ .

Démonstration

L'existence de g {\displaystyle g} $g$ est assurée par le théorème général plus haut. Le fait que g {\displaystyle g} $g$ soit un morphisme de groupes vient du fait que f {\displaystyle f} $f$ et s {\displaystyle s} $s$ sont des morphismes de groupes.

Si H = ker ⁡ f {\displaystyle H=\ker f} $H=\ker f$ , alors f ( x 1 ) = f ( x 2 ) {\displaystyle f(x_{1})=f(x_{2})} $f(x_{1})=f(x_{2})$ si et seulement si x 1 x 2 − 1 ∈ ker ⁡ f = H {\displaystyle x_{1}x_{2}^{-1}\in \ker f=H} $x_{1}x_{2}^{-1}\in \ker f=H$ . Cette dernière condition équivaut à x 1 R x 2 {\displaystyle x_{1}Rx_{2}} $x_{1}Rx_{2}$ . D'après le théorème général, g {\displaystyle g} $g$ est injective.

Le cas des espaces vectoriels

On considère un espace vectoriel E {\displaystyle E} $E$ et la relation d'équivalence définie par un sous-espace vectoriel H {\displaystyle H} $H$ : x R x ′ {\displaystyle xRx'} $xRx'$ si x − x ′ ∈ H {\displaystyle x-x'\in H} $x-x'\in H$ . Alors, la surjection canonique s : E → E / H = E / R {\displaystyle s:E\to E/H=E/R} $s:E\to E/H=E/R$ est linéaire.

Théorème — Soit f : E → F {\displaystyle f:E\to F} $f:E\to F$ une application linéaire. Si H {\displaystyle H} $H$ est contenu dans le noyau de f {\displaystyle f} $f$ , alors il existe une unique application linéaire g : E / H → F {\displaystyle g:E/H\to F} $g:E/H\to F$ telle que f = g ∘ s {\displaystyle f=g\circ s} $f=g\circ s$ . De plus :

g {\displaystyle g} $g$ est surjective si f {\displaystyle f} $f$ est surjective ;
g {\displaystyle g} $g$ est injective si on a H = ker ⁡ f {\displaystyle H=\ker f} $H=\ker f$ ;
g {\displaystyle g} $g$ est un isomorphisme si f {\displaystyle f} $f$ est surjective et H = ker ⁡ f {\displaystyle H=\ker f} $H=\ker f$ .

Le cas des anneaux

Article détaillé : Anneau quotient.

On considère un anneau A {\displaystyle A} $A$ et la relation d'équivalence définie par un idéal bilatère I {\displaystyle I} $I$ de A {\displaystyle A} $A$ : x R x ′ {\displaystyle xRx'} $xRx'$ si x − x ′ ∈ I {\displaystyle x-x'\in I} $x-x'\in I$ . Alors, la surjection canonique s : A → A / I = A / R {\displaystyle s:A\to A/I=A/R} $s:A\to A/I=A/R$ est un morphisme d'anneaux.

Théorème — Soit f : A → B {\displaystyle f:A\to B} $f:A\to B$ un morphisme d'anneaux. Si I {\displaystyle I} $I$ est contenu dans le noyau de f {\displaystyle f} $f$ , alors il existe un unique morphisme d'anneaux g : A / I → B {\displaystyle g:A/I\to B} $g:A/I\to B$ tel que f = g ∘ s {\displaystyle f=g\circ s} $f=g\circ s$ . De plus :

g {\displaystyle g} $g$ est surjectif si f {\displaystyle f} $f$ est surjectif ;
g {\displaystyle g} $g$ est injectif si on a I = ker ⁡ f {\displaystyle I=\ker f} $I=\ker f$ ;
g {\displaystyle g} $g$ est un isomorphisme si f {\displaystyle f} $f$ est surjectif et I = ker ⁡ f {\displaystyle I=\ker f} $I=\ker f$ .

Soit X {\displaystyle X} $X$ un espace topologique muni d'une relation d'équivalence R {\displaystyle R} $R$ et s : X → X / R {\displaystyle s:X\to X/R} $s:X\to X/R$ la surjection canonique. On munit X / R {\displaystyle X/R} $X/R$ de la topologie quotient. Soit f : X → Y {\displaystyle f:X\to Y} $f:X\to Y$ une application continue.

Théorème — Si pour tout couple x R x ′ {\displaystyle xRx'} $xRx'$ dans X {\displaystyle X} $X$ , on a f ( x ) = f ( x ′ ) {\displaystyle f(x)=f(x')} $f(x)=f(x')$ , alors il existe une unique application continue g : X / R → Y {\displaystyle g:X/R\to Y} $g:X/R\to Y$ telle que f = g ∘ s {\displaystyle f=g\circ s} $f=g\circ s$ . De plus :

g {\displaystyle g} $g$ est surjective si f {\displaystyle f} $f$ est surjective ;

g {\displaystyle g} $g$ est injective si on a x R x ′ {\displaystyle xRx'} $xRx'$ équivalent à f ( x ) = f ( x ′ ) {\displaystyle f(x)=f(x')} $f(x)=f(x')$ ;

g {\displaystyle g} $g$ est ouverte (resp. fermée) si f {\displaystyle f} $f$ est ouverte (resp. fermée) ;

g {\displaystyle g} $g$ est un homéomorphisme si f {\displaystyle f} $f$ est surjective et ouverte ou fermée, et si x R x ′ ⟺ f ( x ) = f ( x ′ ) {\displaystyle xRx'\Longleftrightarrow f(x)=f(x')} $xRx'\Longleftrightarrow f(x)=f(x')$ .
Démonstration
La continuité de g {\displaystyle g} $g$ résulte immédiatement des propriétés générales de la topologie quotient. Pour toute partie F {\displaystyle F} $F$ de X / R {\displaystyle X/R} $X/R$ , on a g ( F ) = f ( s − 1 ( F ) ) {\displaystyle g(F)=f(s^{-1}(F))} $g(F)=f(s^{-1}(F))$ , cela implique la propriété sur les applications ouvertes ou fermées.

Références