Système unaire
Dans le monde d'aujourd'hui, Système unaire a fait l'objet de débats et d'analyses dans divers domaines. De la psychologie à la politique, Système unaire a retenu l'attention des experts et des citoyens. Dans un contexte où l’information circule en permanence sur les réseaux sociaux et les médias, il est inévitable d’être curieux de savoir Système unaire et son impact sur notre société. Dans cet article, nous explorerons en détail les implications de Système unaire dans différents domaines, ainsi que les implications possibles pour l'avenir. Sans aucun doute, Système unaire est devenu un élément essentiel dans la vie quotidienne et sa pertinence ne peut être sous-estimée.
Le système unaire aussi appelé système monadique est un système de numération permettant l'écriture des entiers naturels en ne disposant que d'un unique symbole représentant l'unité. Un entier s'écrit par juxtaposition de la quantité correspondante de copies du symbole. Ainsi 6 s'écrit |||||| où | est le symbole utilisé pour représenter l'unité.
Opérations en système unaire
Les opérations s'effectuent ainsi :
- L'addition de deux entiers naturels se traduit par la concaténation des séquences de symboles correspondantes. Ainsi, la somme de ||||| et de |||| est |||||||||.
- La soustraction de deux opérandes s'effectue par élimination d'une copie de la séquence de symboles correspondant à l'entier soustrait. Ainsi, la différence de ||||||||||| par ||||| est
||||||||||| donc ||||||. - La multiplication de deux entiers naturels s'effectue par substitution de chaque apparition du symbole de l'unité dans la séquence du premier entier par une copie de la séquence correspondante au second entier. Ainsi, la multiplication de |||||| par ||| est ||||||||||||||||||.
- La division de deux entiers naturels s'effectue par substitution de chaque apparition de la seconde séquence par le symbole de l'unité, lorsqu'il ne reste plus suffisamment de symboles, le surplus définit le reste. Ainsi, la division de ||||||||||||||||| par |||, donne ||||| pour quotient avec || pour reste.
Pratique du système unaire
Compter sur une main, ou avec des bûchettes comme, est en soi un système unaire. Ce système est aussi beaucoup utilisé dans la représentation populaire du prisonnier. Il compte les jours sur le mur de sa prison en y gravant un trait par jour, ce qui est une utilisation du système unaire.
Les marques de dénombrement sont un exemple où le système unaire est utilisé en pratique. Ils servent à noter les résultats, comme des scores de jeux sportifs, et ne nécessitent pas l'effacement ou le remplacement de l'ancien score. Un point supplémentaire implique l'ajout d'un symbole de l'unité.
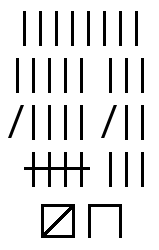
Les marques sont couramment rassemblées en groupes de cinq pour améliorer la lisibilité. Cela est similaire à la pratique d'utiliser un séparateur de milliers (comme une espace, un point ou une virgule) dans l’écriture occidentale usuelle du système décimal, ce qui permet de rendre les nombres tels que 1 234 567 plus faciles à lire. Ces groupes de cinq peuvent être symbolisés par espacement des groupes successifs, éventuellement en ajustant obliquement la première ou dernière marque de chaque groupe, ou encore en barrant le groupe avec la dernière marque.
Le Papyrus de Moscou offre un exemple historique d'une étude mathématique où le système unaire a été utilisé[réf. nécessaire].
Représentation d'un nombre en code unaire
La représentation en code unaire d'un nombre est en fait la conversion d'un nombre binaire en une succession de zéros :
- Le chiffre 0 est transformé en 00 suivi d'un espace et la succession de zéros qui suit correspond au nombre de zéros ;
Exemple : 000 est transformé en 00 000.
- Le chiffre 1 est transformé en 0 et la succession de zéros qui suit correspond au nombre de 1 ;
Exemple : 1111 est transformé en 0 0000.
- Ainsi le nombre 11100110000 se transforme en 0 000 00 00 0 00 00 0000.
On appelle cela la représentation unaire d'un nombre.
Une application de cette représentation fut faite lors d'un concours Codingame (concours de programmation informatique)[1].
L'application classique de la conversion d'un nombre en code unaire est l'utilisation de transfert d'ondes radio.
Arithmétique de Peano
La construction d'une arithmétique nécessite des tables d'additions et des multiplications dont la taille dépend du nombre de chiffres employés dans l'écriture des nombres. Le système unaire offre donc les plus simples définitions de ces opérations. C'est pourquoi, l'arithmétique de Peano, qui est la formalisation mathématique des nombres entiers et de leur arithmétique est basée sur le système unaire : l'unique chiffre | est alors qui doit est appréhendé comme une fonction qui, à tous nombre renvoie son successeur (ou son suivant). Un second symbole sert de marqueur de fin[2]
Ainsi, par exemple :
- Le nombre zéro (le seul nombre sans chiffre) est .
- Le nombre 3 est .
- La formalisation de « la multiplication de deux entiers naturels s'effectue par substitution de chaque apparition du symbole de l'unité dans la séquence du premier entier par une copie de la séquence correspondante au second entier. » est la propriété .
Voir aussi
- Marques de dénombrement, une de ses applications.
Notes et références
- ↑ Codingame
- ↑ Ce marqueur (qui peut être un caractère d'espacement, une virgule, une fin de ligne, etc.) est un symbole surnuméraire indispensable à l'écriture de nombres, et plus généralement de mots. L'invisibilité et la méconnaissance de ce marqueur, ont pour conséquence, la représentation du nombre par le symbole 0 plutôt qu'une absence de chiffres. Cette incongruité viole la règle de suppression des 0 à gauche.




