Fonction porte

Pour les articles homonymes, voir Porte.

Cet article est une ébauche concernant les mathématiques.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

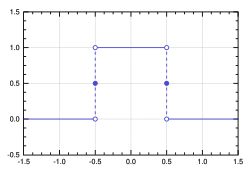
La fonction porte, généralement notée Π, est la fonction indicatrice de l'intervalle réel , c'est-à-dire la fonction mathématique par laquelle un nombre réel a une image nulle, sauf s'il est compris entre –1/2 et 1/2, auquel cas son image vaut 1. Son graphe a une forme similaire à celle d'une porte, d'où son nom.

La fonction porte ${\displaystyle \Pi }$, définie sur les réels et à valeurs dans ${\displaystyle \{0,1\}}$, est définie par :

${\displaystyle \forall t\in \mathbb {R} \quad \Pi (t)={\begin{cases}1&{\text{si }}-1/2\leq t\leq 1/2\\0&{\text{sinon.}}\end{cases}}}$

Par généralisation, on appelle également fonction porte toute fonction déduite par translation et/ou dilatation de la fonction définie ci-dessus. Les notations varient.

La fonction porte peut s'exprimer à l'aide de la fonction de Heaviside par :

${\displaystyle \forall t\in \mathbb {R} \quad \Pi (t)=H\left(t+{\frac {1}{2}}\right)-H\left(t-{\frac {1}{2}}\right)}$.

On peut translater la fonction porte en additionnant ou en soustrayant à t un facteur de translation (attention : la soustraction induit un retard et l'addition induit un avancement par rapport à 0).

On peut élargir la porte de à en divisant t par a dans l'expression de la porte originale.

La dérivée de la fonction porte au sens des distributions s'exprime avec la fonction de Dirac ${\displaystyle \delta (t+1/2)-\delta (t-1/2)}$.

La transformée de Fourier de la fonction porte définie ci-dessus est un sinus cardinal :

${\displaystyle {\mathcal {F}}(\Pi )(f)=\mathrm {sinc} (\pi f)}$^[1].

La fonction porte sert de base pour définir la fonction densité d'une variable aléatoire suivant une loi uniforme continue : si X est une variable aléatoire suivant une loi uniforme continue sur , alors sa fonction densité est :

${\displaystyle f_{X}(x)={\frac {1}{b-a}}\Pi \left({\frac {2x-a-b}{2(b-a)}}\right).}$

• Signal carré
• Fonction de Heaviside
• Approximation sigma
• Fonction triangulaire

• Portail de l'analyse